Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 80, pp. 1-16.
Cyclic approximation to stasis
Stewart D. Johnson, Jordan Rodu
Abstract:
Neighborhoods of points in
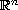 where a positive linear
combination of
where a positive linear
combination of
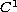 vector fields sum to zero contain,
generically, cyclic trajectories that switch between the vector
fields. Such points are called stasis points, and the
approximating switching cycle can be chosen so that the timing of
the switches exactly matches the positive linear weighting. In the
case of two vector fields, the stasis points form one-dimensional
vector fields sum to zero contain,
generically, cyclic trajectories that switch between the vector
fields. Such points are called stasis points, and the
approximating switching cycle can be chosen so that the timing of
the switches exactly matches the positive linear weighting. In the
case of two vector fields, the stasis points form one-dimensional
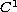 manifolds containing nearby families of two-cycles. The
generic case of two flows in
manifolds containing nearby families of two-cycles. The
generic case of two flows in
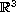 can be diffeomorphed
to a standard form with cubic curves as trajectories.
can be diffeomorphed
to a standard form with cubic curves as trajectories.
Submitted July 27, 2007. Published June 24, 2009.
Math Subject Classifications: 37C10, 37C27.
Key Words: Two-cycles; stasis points; switching systems; piecewise smooth;
relaxed controls.
Show me the PDF file (625 KB),
TEX file, and other files for this article.
 |
Stewart Johnson
Bronfman Science Center, Williams College
Williamstown, MA 01267, USA
email: sjohnson@williams.edu |
|---|
 |
Jordan Rodu
Bronfman Science Center, Williams College
Williamstown, MA 01267, USA
email: jordan.rodu@gmail.com |
|---|
Return to the EJDE web page
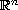 where a positive linear
combination of
where a positive linear
combination of
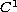 vector fields sum to zero contain,
generically, cyclic trajectories that switch between the vector
fields. Such points are called stasis points, and the
approximating switching cycle can be chosen so that the timing of
the switches exactly matches the positive linear weighting. In the
case of two vector fields, the stasis points form one-dimensional
vector fields sum to zero contain,
generically, cyclic trajectories that switch between the vector
fields. Such points are called stasis points, and the
approximating switching cycle can be chosen so that the timing of
the switches exactly matches the positive linear weighting. In the
case of two vector fields, the stasis points form one-dimensional
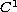 manifolds containing nearby families of two-cycles. The
generic case of two flows in
manifolds containing nearby families of two-cycles. The
generic case of two flows in
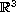 can be diffeomorphed
to a standard form with cubic curves as trajectories.
can be diffeomorphed
to a standard form with cubic curves as trajectories.

