Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 71, pp. 1-7.
Existence of positive solutions for quasilinear elliptic systems
involving the p-Laplacian
Xudong Shang, Jihui Zhang
Abstract:
In this article, we study the existence of positive solutions for
the quasilinear elliptic system
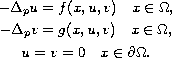
Using degree theoretic arguments based on the degree map for
operators of type
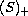 ,
under suitable assumptions on the
nonlinearities, we prove the existence of positive weak solutions.
,
under suitable assumptions on the
nonlinearities, we prove the existence of positive weak solutions.
Submitted March 6, 2009. Published June 1, 2009.
Math Subject Classifications: 34A34, 34B18.
Key Words: p-Laplacian system; positive solutions;
operator of type $(S)_+$.
Show me the PDF file (198 KB),
TEX file, and other files for this article.
 |
Xudong Shang
Department of Mathematics, Nanjing Normal University Taizhou College
Taizhou 225300, Jiangsu, China
email: xudong-shang@163.com
|
|---|
 |
Jihui Zhang
Institute of Mathematics, School of Mathematics and Computer
Sciences
Nanjing Normal University, Nanjing 210097, Jiangsu, China
email: jihuiz@jlonline.com
|
|---|
Return to the EJDE web page
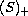 ,
under suitable assumptions on the
nonlinearities, we prove the existence of positive weak solutions.
,
under suitable assumptions on the
nonlinearities, we prove the existence of positive weak solutions.

