Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 70, pp. 1-10.
Growth and oscillation of solutions to linear differential
equations with entire coefficients having the same order
Benharrat Belaidi
Abstract:
In this article, we investigate the growth and
fixed points of solutions of the differential equation
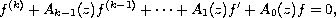
where
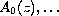 ,
,
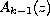 are entire functions.
Some estimates are given for the iterated order and iterated
exponent of convergence of fixed points of solutions of the
above equation when most of the coefficients have the same
order with each other.
are entire functions.
Some estimates are given for the iterated order and iterated
exponent of convergence of fixed points of solutions of the
above equation when most of the coefficients have the same
order with each other.
Submitted February 17, 2009. Published June 1, 2009.
Math Subject Classifications: 34M10, 30D35.
Key Words: Linear differential equation;
growth of entire function; iterated order.
Show me the PDF file (248 KB),
TEX file, and other files for this article.
 |
Benharrat Belaïdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem,
B. P. 227 Mostaganem, Algeria
email: belaidi@univ-mosta.dz, belaidibenharrat@yahoo.fr
|
|---|
Return to the EJDE web page
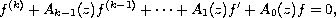
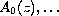 ,
,
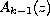 are entire functions.
Some estimates are given for the iterated order and iterated
exponent of convergence of fixed points of solutions of the
above equation when most of the coefficients have the same
order with each other.
are entire functions.
Some estimates are given for the iterated order and iterated
exponent of convergence of fixed points of solutions of the
above equation when most of the coefficients have the same
order with each other.
