Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 43, pp. 1-13.
Multiple positive solutions for a singular elliptic equation
with Neumann boundary condition in two dimensions
Bhatia Sumit Kaur, K. Sreenadh
Abstract:
Let
 be a bounded domain with
be a bounded domain with
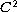 boundary. In this paper, we are interested in the problem
boundary. In this paper, we are interested in the problem
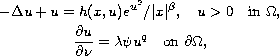
where
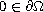 ,
,
 ,
,
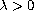 ,
,
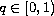 and
and
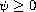 is a H\"older continuous function on
is a H\"older continuous function on
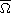 .
Here
.
Here
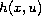 is a
is a
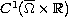 having
superlinear growth at infinity. Using variational methods we show
that there exists
having
superlinear growth at infinity. Using variational methods we show
that there exists
 such that above problem
admits at least two solutions in
such that above problem
admits at least two solutions in
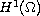 if
if
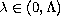 , no solution if
, no solution if
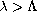 and at least
one solution when
and at least
one solution when
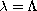 .
.
Submitted August 26, 2008. Published March 24, 2009.
Math Subject Classifications: 34B15, 35J60
Key Words: Multiplicity; nonlinear Neumann boundary condition;
Laplace equation.
Show me the PDF file (280 KB),
TEX file, and other files for this article.
| |
Bhatia Sumit Kaur
Department of Mathematics
Indian Institute of Technology Delhi Hauz Khaz
New Delhi-16, India
email: sumit2212@gmail.com
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi Hauz Khaz
New Delhi-16, India
email: sreenadh@gmail.com
|
|---|
Return to the EJDE web page
 be a bounded domain with
be a bounded domain with
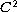 boundary. In this paper, we are interested in the problem
boundary. In this paper, we are interested in the problem
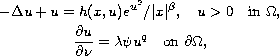
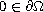 ,
,
 ,
,
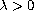 ,
,
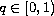 and
and
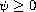 is a H\"older continuous function on
is a H\"older continuous function on
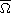 .
Here
.
Here
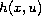 is a
is a
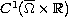 having
superlinear growth at infinity. Using variational methods we show
that there exists
having
superlinear growth at infinity. Using variational methods we show
that there exists
 such that above problem
admits at least two solutions in
such that above problem
admits at least two solutions in
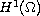 if
if
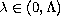 , no solution if
, no solution if
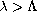 and at least
one solution when
and at least
one solution when
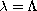 .
.
