In this article, we obtain conditions for the oscillation of vector solutions to the first-order systems of linear difference equations
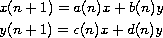
and
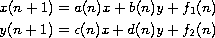
where
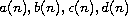 and
and
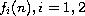 are real valued
functions defined for
are real valued
functions defined for
 .
.
Arun Kumar Tripathy
Abstract:
In this article, we obtain conditions for the oscillation of
vector solutions to the first-order systems of linear difference
equations
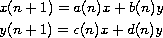
and
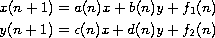
where
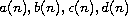 and
and
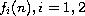 are real valued
functions defined for
are real valued
functions defined for
 .
.
Submitted November 29, 2008. Published February 9, 2009.
Math Subject Classifications: 39A10, 39A12.
Key Words: Oscillation; linear system; difference equation.
Show me the PDF file (226 KB), TEX file, and other files for this article.
 |
Arun Kumar Tripathy Department of Mathematics Kakatiya Institute of Technology and Science Warangal-506015, India email: arun_tripathy70@rediffmail.com |
|---|
Return to the EJDE web page