Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 160, pp. 1-13.
Existence of weak solutions for degenerate semilinear
elliptic equations in unbounded domains
Venkataramanarao Raghavendra, Rasmita Kar
Abstract:
In this study, we prove the existence of a weak solution for
the degenerate semilinear elliptic Dirichlet boundary-value problem

in a suitable weighted Sobolev space.
Here the domain
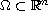 ,
,
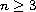 ,
is not necessarily bounded, and
,
is not necessarily bounded, and
 is a continuous bounded
nonlinearity. The theory is also extended for
is a continuous bounded
nonlinearity. The theory is also extended for
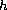 continuous and unbounded.
continuous and unbounded.
Submitted October 25, 2009. Published December 15, 2009.
Math Subject Classifications: 35J70, 35D30.
Key Words: Degenerate equations; weighted Sobolev space; unbounded domain.
Show me the PDF file (260 KB),
TEX file, and other files for this article.
 |
Venkataramanarao Raghavendra
Department of Mathematics and Statistics
Indian Institute of Technology, Kanpur, India 208016
email: vrag@iitk.ac.in
|
|---|
 |
Rasmita Kar
Department of Mathematics and Statistics
Indian Institute of Technology, Kanpur, India 208016
email: rasmita@iitk.ac.in
|
|---|
Return to the EJDE web page

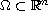 ,
,
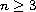 ,
is not necessarily bounded, and
,
is not necessarily bounded, and
 is a continuous bounded
nonlinearity. The theory is also extended for
is a continuous bounded
nonlinearity. The theory is also extended for
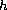 continuous and unbounded.
continuous and unbounded.

