We consider the existence of solutions for the nonlinear second-order two-point ordinary differential equations
![$$\displaylines{
u''(t)+\lambda u(t)+g(u(t))=h(t),\quad t\in[0,1] \cr
u(0)=u(1)=0, \quad\hbox{or} \quad
u'(0)=u'(1)=0
}$$](gifs/aa.gif)
where
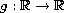 is continuous, and
is continuous, and
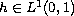 .
.
Rui-Juan Du
Abstract:
We consider the existence of solutions for the nonlinear
second-order two-point ordinary differential equations
![$$\displaylines{
u''(t)+\lambda u(t)+g(u(t))=h(t),\quad t\in[0,1] \cr
u(0)=u(1)=0, \quad\hbox{or} \quad
u'(0)=u'(1)=0
}$$](gifs/aa.gif)
where
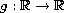 is continuous, and
is continuous, and
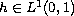 .
.
Submitted May 25, 2009. Published December 15, 2009.
Math Subject Classifications: 34B15.
Key Words: Two-point boundary value problem;
existence; Leray-Schauder theory.
Show me the PDF file (197 KB), TEX file, and other files for this article.
| Rui-Juan Du Department of Computer Science, Gansu Political Science and Law Institute Lanzhou, Gansu, 730070, China email: drjlucky@163.com |
Return to the EJDE web page