Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 153, pp. 1-13.
Existence of solutions for fourth-order PDEs with variable exponents
Abdelrachid El Amrouss, Fouzia Moradi, Mimoun Moussaoui
Abstract:
In this article, we study the following problem with Navier boundary
conditions

Where
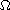 is a bounded domain in
is a bounded domain in
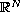 with smooth
boundary
with smooth
boundary
 ,
,
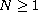 ,
,
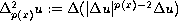 ,
is the
,
is the
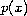 -biharmonic operator,
-biharmonic operator,
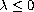 ,
,
 is a continuous function
on
is a continuous function
on
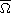 with
with
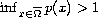 and
and
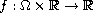 is a Caratheodory function.
Using the Mountain Pass Theorem, we establish the existence of at least
one solution of this problem. Especially, the existence of infinite
many solutions is obtained.
is a Caratheodory function.
Using the Mountain Pass Theorem, we establish the existence of at least
one solution of this problem. Especially, the existence of infinite
many solutions is obtained.
Submitted October 5, 2009. Published November 27, 2009.
Math Subject Classifications: 35G30, 35K61, 46E35.
Key Words: Fourth-order PDEs; variable exponent;
Palais Smale condition; mountain pass theorem;
fountain theorem
Show me the PDF file (256 KB),
TEX file, and other files for this article.
Abdelrachid El Amrouss
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: elamrouss@fso.ump.ma, elamrouss@hotmail.com
|
Fouzia Moradi
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: f.moradi@hotmail.com
|
Mimoun Moussaoui
University Mohamed I, Faculty of sciences
Department of Mathematics, Oujda, Morocco
email: moussaoui@est.ump.ma
|
Return to the EJDE web page

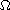 is a bounded domain in
is a bounded domain in
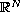 with smooth
boundary
with smooth
boundary
 ,
,
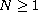 ,
,
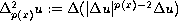 ,
is the
,
is the
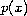 -biharmonic operator,
-biharmonic operator,
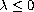 ,
,
 is a continuous function
on
is a continuous function
on
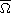 with
with
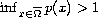 and
and
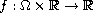 is a Caratheodory function.
Using the Mountain Pass Theorem, we establish the existence of at least
one solution of this problem. Especially, the existence of infinite
many solutions is obtained.
is a Caratheodory function.
Using the Mountain Pass Theorem, we establish the existence of at least
one solution of this problem. Especially, the existence of infinite
many solutions is obtained.