We study the anisotropic boundary-value problem

where
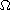 is a smooth bounded domain in
is a smooth bounded domain in
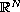
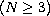 .
We obtain the existence and uniqueness of a weak
energy solution for
.
We obtain the existence and uniqueness of a weak
energy solution for
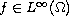 ,
and the existence of weak energy solution for general data
,
and the existence of weak energy solution for general data
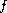 dependent on
dependent on
 .
.
Blaise Kone, Stanislas Ouaro, Sado Traore
Abstract:
We study the anisotropic boundary-value problem

where
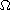 is a smooth bounded domain in
is a smooth bounded domain in
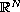
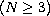 .
We obtain the existence and uniqueness of a weak
energy solution for
.
We obtain the existence and uniqueness of a weak
energy solution for
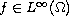 ,
and the existence of weak energy solution for general data
,
and the existence of weak energy solution for general data
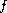 dependent on
dependent on
 .
.
Submitted February 10, 2008. Published November 12, 2009.
Math Subject Classifications: 35J20, 35J25, 35D30, 35B38, 35J60.
Key Words: Anisotropic Sobolev spaces; weak energy solution;
variable exponents; electrorheological fluids.
Show me the PDF file (247 KB), TEX file, and other files for this article.
 |
Blaise Kone Laboratoire d'Analyse Mathématique des Equations (LAME) Institut Burkinabé des Arts et Métiers, Université de Ouagadougou 03 BP 7021 Ouaga 03, Ouagadougou, Burkina Faso email: leizon71@yahoo.fr |
|---|---|
 |
Stanislas Ouaro Laboratoire d'Analyse Mathématique des Equations (LAME) Institut Burkinabé des Arts et Métiers, Université de Ouagadougou 03 BP 7021 Ouaga 03, Ouagadougou, Burkina Faso email: souaro@univ-ouaga.bf, ouaro@yahoo.fr |
 |
Sado Traore Laboratoire d'Analyse Mathématique des Equations (LAME) Institut Burkinabé des Arts et Métiers, Université de Ouagadougou 01 BP 1091 Bobo-Dioulasso 01, email: sado@univ-ouaga.bf |
Return to the EJDE web page