Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 14, pp. 1-5.
Boundedness of solutions for a Lienard
equation with multiple deviating arguments
Yuehua Yu, Changhong Zhao
Abstract:
We consider the Lienard equation
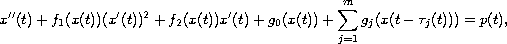
where
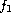 ,
,
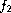 ,
,
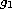 and
and
 are continuous
functions, the delays
are continuous
functions, the delays
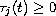 are bounded continuous,
and
are bounded continuous,
and
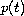 is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
Submitted December 15, 2008. Published January 13, 2009.
Math Subject Classifications: 34C25, 34K13, 34K25.
Key Words: Lienard equation; deviating argument; bounded solution.
Show me the
PDF file (187 KB),
TEX file, and other files for this article.
Yuehua Yu
Department of Mathematics
Hunan University of Arts and Science
Changde, Hunan 415000, China
email: jinli127@yahoo.com.cn |
Changhong Zhao
Department of Mathematics
Hunan University of Arts and Science
Changde, Hunan 415000, China
email: hongchangzhao@yahoo.com.cn |
Return to the EJDE web page
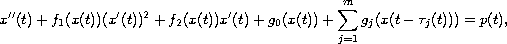
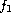 ,
,
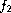 ,
,
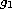 and
and
 are continuous
functions, the delays
are continuous
functions, the delays
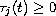 are bounded continuous,
and
are bounded continuous,
and
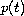 is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.