Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 131, pp. 1-16.
Multiple solutions for nonlinear elliptic equations on
Riemannian manifolds
Wenjing Chen, Jianfu Yang
Abstract:
Let
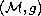 be a compact, connected, orientable,
Riemannian
be a compact, connected, orientable,
Riemannian
 -manifold of class
-manifold of class
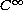 with Riemannian metric
with Riemannian metric

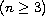 .
We study the
existence of solutions to the equation
.
We study the
existence of solutions to the equation
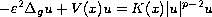
on this Riemannian manifold. Here
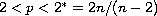 ,
,
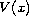 and
and
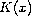 are continuous functions. We show that the shape
of
are continuous functions. We show that the shape
of
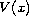 and
and
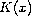 affects the number of solutions,
and then prove the existence of multiple solutions.
affects the number of solutions,
and then prove the existence of multiple solutions.
Submitted September 15, 2009. Published October 9, 2009.
Math Subject Classifications: 35J20, 35J61, 58J05.
Key Words: Multiple Solutions; Semilinear elliptic equation;
Riemannian manifold; Ljusternik-Schnirelmann category.
Show me the PDF file (302 KB),
TEX file, and other files for this article.
Wenjing Chen
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi, 330022, China
email: wjchen1102@yahoo.com.cn
|
Jianfu Yang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi, 330022, China
email: jfyang_2000@yahoo.com
|
Return to the EJDE web page
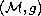 be a compact, connected, orientable,
Riemannian
be a compact, connected, orientable,
Riemannian
 -manifold of class
-manifold of class
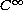 with Riemannian metric
with Riemannian metric

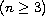 .
We study the
existence of solutions to the equation
.
We study the
existence of solutions to the equation
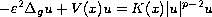
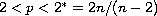 ,
,
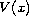 and
and
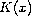 are continuous functions. We show that the shape
of
are continuous functions. We show that the shape
of
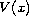 and
and
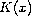 affects the number of solutions,
and then prove the existence of multiple solutions.
affects the number of solutions,
and then prove the existence of multiple solutions.