We study the singular boundary-value problem
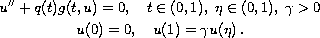
The singularity may appear at
 and the function
and the function
 may
be superlinear at infinity and may change sign.
The existence of solutions is obtained via an upper and lower
solutions method.
may
be superlinear at infinity and may change sign.
The existence of solutions is obtained via an upper and lower
solutions method.
Qiumei Zhang, Daqing Jiang, Shiyou Weng, Haiyin Gao
Abstract:
We study the singular boundary-value problem
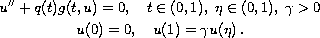
The singularity may appear at
 and the function
and the function
 may
be superlinear at infinity and may change sign.
The existence of solutions is obtained via an upper and lower
solutions method.
may
be superlinear at infinity and may change sign.
The existence of solutions is obtained via an upper and lower
solutions method.
Submitted January 27, 2009. Published September 12, 2009.
Math Subject Classifications: 34B15, 34B16.
Key Words: Singular boundary-value problem; upper and lower solutions;
existence of solutions; superlinear.
Editors note (December 22, 2009):
The result here seems to be particular case of results
previously published by the first two authors
(using exactly the same methods).
Qiumei Zhang, Daqing Jiang, Upper and lower solutions method
and a second order three-point singular boundary value problem,
Computers and Mathematics with Applications 56 (2008) 1059-1070.
(Received 26 July 2007; accepted 7 January 2008).
Readers should check the validity of this claim, but
should not follow this example.
Show me the PDF file (223 KB), TEX file, and other files for this article.
 |
Qiumei Zhang School of Science, Changchun University, Changchun 130022, China. Department of Mathematics, Northeast Normal University Changchun 130024, China email: zhangqm1110@yahoo.com.cn |
|---|---|
 |
Daqing Jiang Department of Mathematics, Northeast Normal University Changchun 130024, China email: jiangdq067@nenu.edu.cn |
 |
Haiyin Gao School of Science, Changchun University Changchun 130022, China email: gaohaiyinhealthy@yahoo.com.cn |
 |
Shiyou Weng School of Science, Changchun University Changchun 130022, China email: wengshiyou2001@yahoo.com.cn |
Return to the EJDE web page