Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 11, pp. 1-11.
Existence and uniqueness of positive solutions for a
BVP with a p-Laplacian on the half-line
Yu Tian, Weigao Ge
Abstract:
In this work, we consider the second order multi-point
boundary-value problem with a p-Laplacian
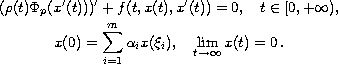
By applying a nonlinear alternative theorem,
we establish existence and uniqueness of solutions on the half-line.
Also a uniqueness result for positive solutions is discussed
when
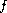 depends on the first-order derivative. The emphasis here
is on the one dimensional p-Laplacian operator.
depends on the first-order derivative. The emphasis here
is on the one dimensional p-Laplacian operator.
Submitted May 23, 2008. Published January 9, 2009.
Math Subject Classifications: 34B10, 34B18, 34B40.
Key Words: Multi-point boundary-value problem; p-Laplacian;
half-line; positive solutions; existence; uniqueness.
Show me the
PDF file (232 KB),
TEX file, and other files for this article.
 |
Yu Tian
School of Science
Beijing University of Posts and Telecommunications
Beijing 100876, China
email: tianyu2992@163.com |
|---|
 |
Weigao Ge
Department of Mathematics
Beijing Institute of Technology
Beijing 100081, China
email: gew@bit.edu.cn
|
|---|
Return to the EJDE web page
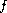 depends on the first-order derivative. The emphasis here
is on the one dimensional p-Laplacian operator.
depends on the first-order derivative. The emphasis here
is on the one dimensional p-Laplacian operator.

