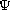 -bounded
solutions for linear differential
systems with Lebesgue
-bounded
solutions for linear differential
systems with Lebesgue
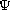 -integrable
functions on
-integrable
functions on
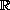 as right-hand sides
as right-hand sides
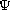 -bounded
solutions for linear differential
systems with Lebesgue
-bounded
solutions for linear differential
systems with Lebesgue
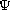 -integrable
functions on
-integrable
functions on
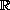 as right-hand sides
as right-hand sides
Aurel Diamandescu
Abstract:
In this paper we give a characterization for the existence
of
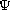 -bounded
solutions on
-bounded
solutions on
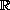 for the system
for the system
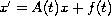 ,
assuming that f is a Lebesgue
,
assuming that f is a Lebesgue
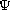 -integrable
function on
-integrable
function on
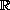 .
In addition, we give a result in connection
with the asymptotic behavior of the
.
In addition, we give a result in connection
with the asymptotic behavior of the
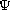 -bounded
solutions of this system.
-bounded
solutions of this system.
Submitted October 9, 2008. Published January 6, 2009.
Math Subject Classifications: 34D05, 34C11.
Key Words: Psi-bounded; Psi-integrable.
Show me the PDF file (215 KB), TEX file, and other files for this article.
 |
Aurel Diamandescu University of Craiova Department of Applied Mathematics 13, ``Al. I. Cuza'' st., 200585, Craiova, Romania email: adiamandescu@central.ucv.ro |
|---|
Return to the EJDE web page