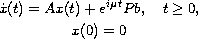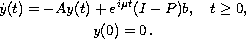Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 94, pp. 1-5.
A characterization of dichotomy in terms of boundedness of solutions
for some Cauchy problems
Akbar Zada
Abstract:
We prove that a quadratic matrix of order
 having complex
entries is dichotomic (i.e. its spectrum does not intersect
the imaginary axis) if and only if there exists a projection
having complex
entries is dichotomic (i.e. its spectrum does not intersect
the imaginary axis) if and only if there exists a projection
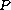 on
on
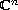 such that
such that
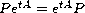 for all
for all
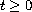 and for each real number
and for each real number
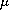 and each vector
and each vector
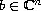 the solutions of the following
two Cauchy problems are bounded:
the solutions of the following
two Cauchy problems are bounded:
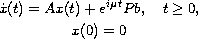
and
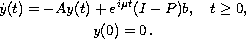
Submitted May 29, 2008. Published July 05, 2008.
Math Subject Classifications: 47D06, 35B35.
Key Words: Stable and dichotomic matrices; Cauchy problem;
spectral decomposition theorem.
Show me the
PDF file (183 KB),
TEX file, and other files for this article.
 |
Akbar Zada
Government College University
Abdus Salam School of Mathematical Sciences, (ASSMS)
Lahore, Pakistan
email: zadababo@yahoo.com |
|---|
Return to the EJDE web page
 having complex
entries is dichotomic (i.e. its spectrum does not intersect
the imaginary axis) if and only if there exists a projection
having complex
entries is dichotomic (i.e. its spectrum does not intersect
the imaginary axis) if and only if there exists a projection
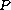 on
on
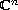 such that
such that
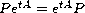 for all
for all
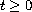 and for each real number
and for each real number
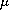 and each vector
and each vector
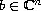 the solutions of the following
two Cauchy problems are bounded:
the solutions of the following
two Cauchy problems are bounded: