Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 87, pp. 1-10.
Positive solutions to nonlinear second-order three-point boundary-value
problems for difference equation with change of sign
Chunli Wang, Xiaoshuang Han, Chunhong Li
Abstract:
In this paper we investigate the existence of positive solution to
the discrete second-order three-point boundary-value problem
![$$\displaylines{
\Delta^2 x_{k-1}+ h(k) f(x_k)=0, \quad k \in [1, n], \cr
x_0 =0, \quad a x_l = x_{n+1},
}$$](gifs/aa.gif)
where
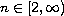 ,
,
![$l \in [1, n]$](gifs/ac.gif) ,
,
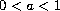 ,
,
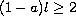 ,
,
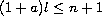 ,
,
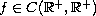 and
and
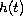 is a function that may change sign on
is a function that may change sign on
![$[1, n]$](gifs/ai.gif) .
Using the fixed-point index theory, we prove the existence of
positive solution for the above boundary-value problem.
.
Using the fixed-point index theory, we prove the existence of
positive solution for the above boundary-value problem.
Submitted March 6, 2008. Published June 11, 2008.
Math Subject Classifications: 39A05, 39A10.
Key Words: Boundary value problem; positive solution;
difference equation; fixed point; changing sign coefficients.
Show me the
PDF file (218 KB),
TEX file, and other files for this article.
 |
Chunli Wang
Institute of Information Technology
University of Electronic Technology
Guilin, Guangxi 541004, China
email: wangchunliwcl821222@sina.com |
|---|
 |
Xiaoshuang Han
Yanbian University of Science and Technology
Yanji, Jilin 133000, China
email: petty_hxs@hotmail.com |
|---|
 |
Chunhong Li
Department of Mathematics
Yanbian University
Yanji, Jilin 133000, China
email: abbccc2007@163.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
\Delta^2 x_{k-1}+ h(k) f(x_k)=0, \quad k \in [1, n], \cr
x_0 =0, \quad a x_l = x_{n+1},
}$$](gifs/aa.gif)
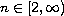 ,
,
![$l \in [1, n]$](gifs/ac.gif) ,
,
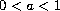 ,
,
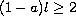 ,
,
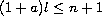 ,
,
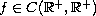 and
and
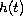 is a function that may change sign on
is a function that may change sign on
![$[1, n]$](gifs/ai.gif) .
Using the fixed-point index theory, we prove the existence of
positive solution for the above boundary-value problem.
.
Using the fixed-point index theory, we prove the existence of
positive solution for the above boundary-value problem.


