Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 84, pp. 1-12.
Stabilized quasi-reversibility method for
a class of nonlinear ill-posed problems
Dang Duc Trong, Nguyen Huy Tuan
Abstract:
In this paper, we study a final value problem for the nonlinear
parabolic equation

where
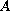 is a non-negative, self-adjoint operator and
is a non-negative, self-adjoint operator and
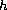 is a Lipchitz function. Using the stabilized quasi-reversibility
method presented by Miller, we find optimal perturbations, of
the operator
is a Lipchitz function. Using the stabilized quasi-reversibility
method presented by Miller, we find optimal perturbations, of
the operator
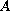 ,
depending on a small parameter
,
depending on a small parameter
 to setup
an approximate nonlocal problem. We show that the approximate problems
are well-posed under certain conditions and that their solutions
converges if and only if the original problem has a classical solution.
We also obtain estimates for the solutions of the approximate problems,
and show a convergence result. This paper extends the work by Hetrick
and Hughes [11] to nonlinear ill-posed problems.
to setup
an approximate nonlocal problem. We show that the approximate problems
are well-posed under certain conditions and that their solutions
converges if and only if the original problem has a classical solution.
We also obtain estimates for the solutions of the approximate problems,
and show a convergence result. This paper extends the work by Hetrick
and Hughes [11] to nonlinear ill-posed problems.
Submitted April 28, 2008. Published June 8, 2008.
Math Subject Classifications: 35K05, 35K99, 47J06, 47H10.
Key Words: Ill-posed problem; nonlinear parabolic equation;
quasi-reversibility methods;
stabilized quasi-reversibility methods.
Show me the
PDF file (243 KB),
TEX file, and other files for this article.
 |
Dang Duc Trong
Department of Mathematics and Informatics
Hochiminh City National University
227 Nguyen Van Cu, Q. 5, Hochiminh City, Vietnam
email: ddtrong@mathdep.hcmuns.edu.vn |
|---|
 |
Nguyen Huy Tuan
Department of Mathematics and Informatics
Ton Duc Thang University
98 Ngo Tat To street , Binh Thanh district Hochiminh City, Vietnam
email: tuanhuy_bs@yahoo.com |
|---|
Return to the EJDE web page

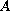 is a non-negative, self-adjoint operator and
is a non-negative, self-adjoint operator and
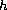 is a Lipchitz function. Using the stabilized quasi-reversibility
method presented by Miller, we find optimal perturbations, of
the operator
is a Lipchitz function. Using the stabilized quasi-reversibility
method presented by Miller, we find optimal perturbations, of
the operator
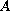 ,
depending on a small parameter
,
depending on a small parameter
 to setup
an approximate nonlocal problem. We show that the approximate problems
are well-posed under certain conditions and that their solutions
converges if and only if the original problem has a classical solution.
We also obtain estimates for the solutions of the approximate problems,
and show a convergence result. This paper extends the work by Hetrick
and Hughes [11] to nonlinear ill-posed problems.
to setup
an approximate nonlocal problem. We show that the approximate problems
are well-posed under certain conditions and that their solutions
converges if and only if the original problem has a classical solution.
We also obtain estimates for the solutions of the approximate problems,
and show a convergence result. This paper extends the work by Hetrick
and Hughes [11] to nonlinear ill-posed problems.

