Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 81, pp. 1-11.
Existence results for strongly indefinite elliptic systems
Jianfu Yang, Ying Ye, Xiaohui Yu
Abstract:
In this paper, we show the existence of solutions for
the strongly indefinite elliptic system
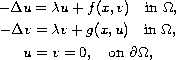
where
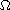 is a bounded domain in
is a bounded domain in
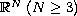 with smooth
boundary,
with smooth
boundary,
 ,
where
,
where
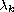 is
the
is
the
 th
eigenvalue of
th
eigenvalue of
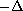 in
in
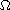 with zero Dirichlet
boundary condition. Both cases when
with zero Dirichlet
boundary condition. Both cases when
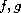 being superlinear and
asymptotically linear at infinity are considered.
being superlinear and
asymptotically linear at infinity are considered.
Submitted April l7, 2008. Published May 28, 2008.
Math Subject Classifications: 35J20,3 5J25.
Key Words: Strongly indefinite elliptic system; existence.
Show me the
PDF file (241 KB),
TEX file, and other files for this article.
Jianfu Yang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com |
Ying Ye
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: yeying19851985@163.com |
Xiaohui Yu
China Institute for Advanced Study
Central University of Finance and Economics
Beijing 100081, China
email: yuxiao_211@163.com
|
Return to the EJDE web page
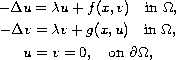
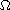 is a bounded domain in
is a bounded domain in
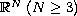 with smooth
boundary,
with smooth
boundary,
 ,
where
,
where
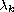 is
the
is
the
 th
eigenvalue of
th
eigenvalue of
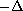 in
in
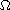 with zero Dirichlet
boundary condition. Both cases when
with zero Dirichlet
boundary condition. Both cases when
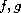 being superlinear and
asymptotically linear at infinity are considered.
being superlinear and
asymptotically linear at infinity are considered.