Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 64, pp. 1-15.
Matrix elements for sum of power-law potentials in
quantum mechanic using generalized hypergeometric functions
Qutaibeh D. Katatbeh, Ma'zoozeh E. Abu-Amra
Abstract:
In this paper we derive close form for the matrix elements for
 , where
, where
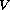 is a pure power-law potential.
We use trial functions of the form
is a pure power-law potential.
We use trial functions of the form

for
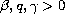 to obtain the matrix elements for
to obtain the matrix elements for
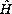 .
These formulas are then optimized with respect to variational
parameters
.
These formulas are then optimized with respect to variational
parameters
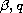 and
and
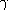 to obtain accurate upper
bounds for the given nonsolvable eigenvalue problem in quantum mechanics.
Moreover, we write the matrix elements in terms of the generalized
hypergeomtric functions. These results are generalization of those
found earlier in [2], [8-16] for power-law potentials.
Applications and comparisons with earlier work are presented.
to obtain accurate upper
bounds for the given nonsolvable eigenvalue problem in quantum mechanics.
Moreover, we write the matrix elements in terms of the generalized
hypergeomtric functions. These results are generalization of those
found earlier in [2], [8-16] for power-law potentials.
Applications and comparisons with earlier work are presented.
Submitted February 19, 2008 Published April 28, 2008.
Math Subject Classifications: 34L15, 34L16, 81Q10, 35P15.
Key Words: Schrodinger equation; variational technique;
eigenvalues; upper bounds; analytical computations.
Show me the
PDF file (258 KB),
TEX file, and other files for this article.
 |
Qutaibeh D. Katatbeh
Department of Mathematics and Statistics,
Faculty of Science and Arts
Jordan University of Science and Technology
Irbid 22110, Jordan
email: qutaibeh@yahoo.com |
|---|
 |
Ma'zoozeh E. Abu-Amra
Department of Mathematics and Statistics,
Faculty of Science and Arts
Jordan University of Science and Technology
Irbid 22110, Jordan |
|---|
Return to the EJDE web page
 , where
, where
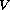 is a pure power-law potential.
We use trial functions of the form
is a pure power-law potential.
We use trial functions of the form

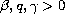 to obtain the matrix elements for
to obtain the matrix elements for
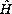 .
These formulas are then optimized with respect to variational
parameters
.
These formulas are then optimized with respect to variational
parameters
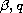 and
and
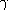 to obtain accurate upper
bounds for the given nonsolvable eigenvalue problem in quantum mechanics.
Moreover, we write the matrix elements in terms of the generalized
hypergeomtric functions. These results are generalization of those
found earlier in [2], [8-16] for power-law potentials.
Applications and comparisons with earlier work are presented.
to obtain accurate upper
bounds for the given nonsolvable eigenvalue problem in quantum mechanics.
Moreover, we write the matrix elements in terms of the generalized
hypergeomtric functions. These results are generalization of those
found earlier in [2], [8-16] for power-law potentials.
Applications and comparisons with earlier work are presented.

