Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 62, pp. 1-11.
On boundary-value problems for higher-order differential inclusions
Myelkebir Aitalioubrahim, Said Sajid
Abstract:
We show the existence of solutions to boundary-value problems
for higher-order differential inclusion
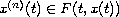 , where
, where
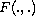 is a closed
multifunction, measurable in
is a closed
multifunction, measurable in
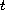 and Lipschitz continuous in
and Lipschitz continuous in
 .
We use the fixed point theorem introduced by Covitz and Nadler for
contraction multivalued maps.
.
We use the fixed point theorem introduced by Covitz and Nadler for
contraction multivalued maps.
Submitted March 14, 2007. Published April 22, 2008.
Math Subject Classifications: 34A60, 34B10, 34B15.
Key Words: Boundary value problems; contraction;
measurability; multifunction.
Show me the
PDF file (205 KB),
TEX file, and other files for this article.
 |
Myelkebir Aitalioubrahim
University Hassan II-Mohammedia, U.F.R Mathematics and
applications
F.S.T, B P 146, Mohammedia, Morocco
email: aitalifr@yahoo.fr
|
|---|
 |
Said Sajid
University Hassan II-Mohammedia, U.F.R Mathematics and
applications
F.S.T, B P 146, Mohammedia, Morocco
email: saidsajid@hotmail.com
|
|---|
Return to the EJDE web page
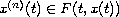 , where
, where
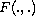 is a closed
multifunction, measurable in
is a closed
multifunction, measurable in
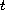 and Lipschitz continuous in
and Lipschitz continuous in
 .
We use the fixed point theorem introduced by Covitz and Nadler for
contraction multivalued maps.
.
We use the fixed point theorem introduced by Covitz and Nadler for
contraction multivalued maps.

