Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 60, pp. 1-9.
Almost automorphy of semilinear parabolic evolution equations
Mahmoud Baroun, Said Boulite, Gaston M. N'Guerekata, Lahcen Maniar
Abstract:
This paper studies the existence and uniqueness of almost
automorphic mild solutions to the semilinear parabolic
evolution equation
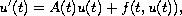
assuming that the linear operators
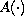 satisfy the
Acquistapace-Terreni conditions, the evolution family
generated by
satisfy the
Acquistapace-Terreni conditions, the evolution family
generated by
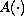 has an exponential dichotomy, and
the resolvent
has an exponential dichotomy, and
the resolvent
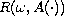 , and
, and
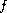 are almost automorphic.
are almost automorphic.
Submitted December 19, 2007. Published April 22, 2008.
Math Subject Classifications: 34G10, 47D06.
Key Words: Parabolic evolution equations; almost automorphy;
exponential dichotomy; Green's function.
Show me the
PDF file (236 KB),
TEX file, and other files for this article.
 |
Mahmoud Baroun
Department of Mathematics,
University Cadi Ayyad
Faculty of Sciences Semlalia
B.P. 2390, 40000 Marrakesh, Morocco
email: m.baroun@ucam.ac.ma |
|---|
 |
Said Boulite
Department of Mathematics,
University Cadi Ayyad
Faculty of Sciences Semlalia
B.P. 2390, 40000 Marrakesh, Morocco
email: sboulite@ucam.ac.ma |
|---|
 |
Gaston M. N'Guérékata
Department of Mathematics
Morgan State University
Baltimore, MD 21251, USA
email: Gaston.N'Guerekata@morgan.edu |
|---|
 |
Lahcen Maniar
Department of Mathematics,
University Cadi Ayyad
Faculty of Sciences Semlalia
B.P. 2390, 40000 Marrakesh, Morocco
email: maniar@ucam.ac.ma |
|---|
Return to the EJDE web page
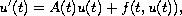
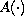 satisfy the
Acquistapace-Terreni conditions, the evolution family
generated by
satisfy the
Acquistapace-Terreni conditions, the evolution family
generated by
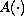 has an exponential dichotomy, and
the resolvent
has an exponential dichotomy, and
the resolvent
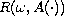 , and
, and
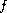 are almost automorphic.
are almost automorphic.



