Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 45, pp. 1-12.
Multiple positive solutions for nonlinear second-order m-point
boundary-value problems with sign changing nonlinearities
Fuyi Xu, Zhenbo Chen, Feng Xu
Abstract:
In this paper, we study the nonlinear second-order m-point
boundary value problem
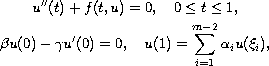
where the nonlinear term
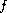 is allowed to change sign.
We impose growth conditions on
is allowed to change sign.
We impose growth conditions on
 which yield the existence of at
least two positive solutions by using a fixed-point theorem
in double cones. Moreover, the associated Green's function for
the above problem is given.
which yield the existence of at
least two positive solutions by using a fixed-point theorem
in double cones. Moreover, the associated Green's function for
the above problem is given.
Submitted December 27, 2007. Published March 29, 2008.
Math Subject Classifications: 34B15.
Key Words: m-point; boundary-value problem; Green's function;
fixed point theorem in double cones.
Show me the
PDF file (236 KB),
TEX file, and other files for this article.
 |
Fuyi Xu
School of Mathematics and Information Science
Shandong University of Technology
Zibo, Shandong, 255049, China
email: zbxufuyi@163.com |
|---|
 |
Zhenbo Chen
School of Mathematics and Information Science
Shandong University of Technology
Zibo, Shandong, 255049, China
email: czb56@sdut.edu.cn |
|---|
 |
Feng Xu
School of Mathematics and Information Science
Shandong University of Technology
Zibo, Shandong, 255049, China
email: zbxf878@126.com |
|---|
Return to the EJDE web page
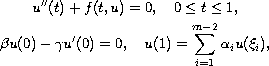
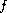 is allowed to change sign.
We impose growth conditions on
is allowed to change sign.
We impose growth conditions on
 which yield the existence of at
least two positive solutions by using a fixed-point theorem
in double cones. Moreover, the associated Green's function for
the above problem is given.
which yield the existence of at
least two positive solutions by using a fixed-point theorem
in double cones. Moreover, the associated Green's function for
the above problem is given.


