Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 37, pp. 1-18.
Multiple semiclassical states for singular magnetic
nonlinear Schrodinger equations
Sara Barile
Abstract:
By means of a finite-dimensional reduction, we show
a multiplicity result of semiclassical solutions
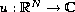 to the singular nonlinear Schrodinger equation
to the singular nonlinear Schrodinger equation
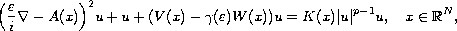
where
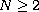 ,
,
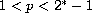 ,
,
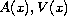 and
and
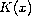 are bounded potentials. Such solutions concentrate near
(non-degenerate) local extrema or a
(non-degenerate) manifold of stationary points of an
auxiliary function
are bounded potentials. Such solutions concentrate near
(non-degenerate) local extrema or a
(non-degenerate) manifold of stationary points of an
auxiliary function
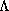 related to the unperturbed electric field
related to the unperturbed electric field
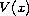 and the coefficient
and the coefficient
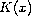 of the nonlinear term.
of the nonlinear term.
Submitted November 26, 2007. Published March 14, 2008.
Math Subject Classifications: 35J10, 35J60, 35J20, 35Q55, 58E05.
Key Words: Nonlinear Schrodinger equations; external magnetic field;
singular potentials; semiclassical limit.
Show me the
PDF file (328 KB),
TEX file, and other files for this article.
 |
Sara Barile
Dipartimento di Matematica, Politecnico di Bari
Via Orabona 4, I-70125 Bari, Italy
email: s.barile@dm.uniba.it |
|---|
Return to the EJDE web page
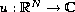 to the singular nonlinear Schrodinger equation
to the singular nonlinear Schrodinger equation
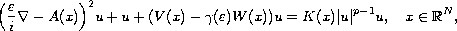
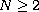 ,
,
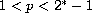 ,
,
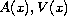 and
and
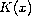 are bounded potentials. Such solutions concentrate near
(non-degenerate) local extrema or a
(non-degenerate) manifold of stationary points of an
auxiliary function
are bounded potentials. Such solutions concentrate near
(non-degenerate) local extrema or a
(non-degenerate) manifold of stationary points of an
auxiliary function
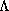 related to the unperturbed electric field
related to the unperturbed electric field
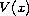 and the coefficient
and the coefficient
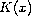 of the nonlinear term.
of the nonlinear term.
