Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 30, pp. 1-18.
Degenerate stationary problems with homogeneous
boundary conditions
Kaouther Ammar, Hicham Redwane
Abstract:
We are interested in the degenerate problem
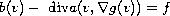
with the homogeneous boundary condition
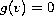 on some part of the boundary.
The vector field
on some part of the boundary.
The vector field
 is supposed to satisfy the
Leray-Lions conditions and the functions
is supposed to satisfy the
Leray-Lions conditions and the functions
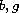 to be continuous,
nondecreasing and to verify the normalization condition
to be continuous,
nondecreasing and to verify the normalization condition
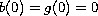 and the range condition
and the range condition
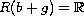 .
Using monotonicity methods, we prove existence and
comparison results for renormalized entropy solutions in
the
.
Using monotonicity methods, we prove existence and
comparison results for renormalized entropy solutions in
the
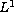 setting.
setting.
Submitted January 8, 2008. Published February 28. 2008.
Math Subject Classifications: 35K65, 35F30, 35K35, 65M12.
Key Words: Degenerate; homogenous boundary conditions; diffusion;
continuous flux.
Show me the
PDF file (289 KB),
TEX file, and other files for this article.
 |
Kaouther Ammar
TU Berlin, Institut für Mathematik, MA 6-3
Strasse des 17. Juni 136, 10623 Berlin, Germany
email: ammar@math.tu-berlin.de, Fax:+4931421110, Tel: +4931429306
|
|---|
 |
Hicham Redwane
Faculté des sciences juridiques, Economiques et Sociales
Université Hassan 1
B.P. 784, Settat, Morocco
email: redwane_hicham@yahoo.fr |
|---|
Return to the EJDE web page
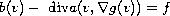
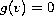 on some part of the boundary.
The vector field
on some part of the boundary.
The vector field
 is supposed to satisfy the
Leray-Lions conditions and the functions
is supposed to satisfy the
Leray-Lions conditions and the functions
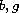 to be continuous,
nondecreasing and to verify the normalization condition
to be continuous,
nondecreasing and to verify the normalization condition
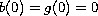 and the range condition
and the range condition
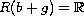 .
Using monotonicity methods, we prove existence and
comparison results for renormalized entropy solutions in
the
.
Using monotonicity methods, we prove existence and
comparison results for renormalized entropy solutions in
the
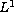 setting.
setting.

