Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 25, pp. 1-6.
Existence of solutions for some third-order
boundary-value problems
Zhanbing Bai
Abstract:
In this paper concerns the third-order boundary-value problem
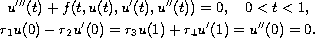
By placing certain restrictions on the nonlinear term f,
we prove the existence of at least one solution to the
boundary-value problem with the use of lower and upper solution
method and of Schauder fixed-point theorem.
The construction of lower or upper solutions is also presented.
Submitted September 21, 2007. Published February 22, 2008.
Math Subject Classifications: 34B15.
Key Words: Third-order boundary-value problem;
lower and upper solutions; fixed-point theorem.
Show me the
PDF file (189 KB),
TEX file, and other files for this article.
 |
Zhanbing Bai
Institute of Mathematics
Shandong University of Science and Technology
Qingdao 266510, China
email: zhanbingbai@163.com |
|---|
Return to the EJDE web page