Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 165, pp. 1-6.
Multiple solutions for quasilinear elliptic problems with
nonlinear boundary conditions
Nguyen Thanh Chung
Abstract:
Using a recent result by Bonanno [2], we obtain a
multiplicity result for the quasilinear elliptic problem
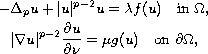
where
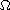 is a bounded domain in
is a bounded domain in
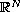 ,
,
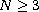 with smooth boundary
with smooth boundary
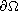 ,
,
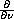 is the outer unit normal derivative,
the functions
is the outer unit normal derivative,
the functions
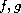 are
are
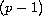 -sublinear
at infinity
(
-sublinear
at infinity
(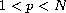 ),
),
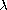 and
and
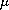 are positive parameters.
are positive parameters.
Submitted October 20, 2008. Published December 23, 2008.
Math Subject Classifications: 35J65, 35J20.
Key Words: Multiple solutions; quasilinear elliptic problems;
nonlinear boundary conditions
Show me the
PDF file (213 KB),
TEX file, and other files for this article.
 |
Nguyen Thanh Chung
Department of Mathematics and Informatics
Quang Binh University
312 Ly Thuong Kiet, Dong Hoi, Quang Binh, Vietnam
email: ntchung82@yahoo.com
|
|---|
Return to the EJDE web page
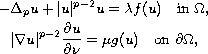
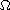 is a bounded domain in
is a bounded domain in
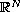 ,
,
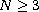 with smooth boundary
with smooth boundary
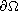 ,
,
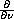 is the outer unit normal derivative,
the functions
is the outer unit normal derivative,
the functions
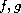 are
are
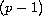 -sublinear
at infinity
(
-sublinear
at infinity
(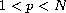 ),
),
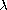 and
and
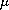 are positive parameters.
are positive parameters.
