Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 159, pp. 1-10.
Multiple positive solutions of fourth-order four-point
boundary-value problems with changing sign coefficient
Zheng Fang, Chunhong Li, Chuanzhi Bai
Abstract:
In this paper, we investigate the existence of multiple positive
solutions of the fourth-order four-point boundary-value problems
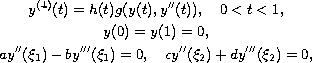
where
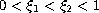 . We show the existence of three
positive solutions by applying the Avery and Peterson fixed point
theorem in a cone, here
. We show the existence of three
positive solutions by applying the Avery and Peterson fixed point
theorem in a cone, here
 may change sign on
may change sign on
![$[0, 1]$](gifs/ad.gif) .
.
Submitted September 3, 2008. Published December 3, 2008.
Math Subject Classifications: 34B10, 34B15.
Key Words: Four-point boundary-value problem; positive solution;
fixed point on a cone.
Show me the
PDF file (208 KB),
TEX file, and other files for this article.
| |
Zheng Fang
School of Science,
Jiangnan University
Wuxi, Jiangsu 214122, China
email: fangzhengm@yahoo.com.cn |
|---|
 |
Chunhong Li
Department of Mathematics,
Huaiyin Teachers College
Huaian, Jiangsi 223300, China
email: lichshy2006@126.com |
|---|
 |
Chuanzhi Bai
Department of Mathematics,
Huaiyin Teachers College
Huaian, Jiangsi 223300, China
email: czbai8@sohu.com |
|---|
Return to the EJDE web page
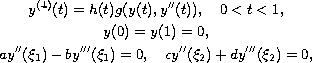
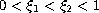 . We show the existence of three
positive solutions by applying the Avery and Peterson fixed point
theorem in a cone, here
. We show the existence of three
positive solutions by applying the Avery and Peterson fixed point
theorem in a cone, here
 may change sign on
may change sign on
![$[0, 1]$](gifs/ad.gif) .
.

