Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 137, pp. 1-18.
Integral representation of solutions to boundary-value problems
on the half-line for linear ODEs with singularity of the first kind
Yulia Horishna, Igor Parasyuk, Lyudmyla Protsak
Abstract:
We study the existence of solutions
to a non-homogeneous system of linear ODEs which
has the pole of first order at
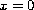 ;
these solutions should
vanish at infinity and be continuously differentiable on
;
these solutions should
vanish at infinity and be continuously differentiable on
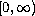 .
The resonant case where the corresponding homogeneous problem
has nontrivial solutions is of great interest to us.
Under the conditions that the homogeneous system is exponentially
dichotomic on
.
The resonant case where the corresponding homogeneous problem
has nontrivial solutions is of great interest to us.
Under the conditions that the homogeneous system is exponentially
dichotomic on
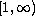 and the residue of system's
operator at
and the residue of system's
operator at
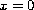 does not have eigenvalues with real part 1, we
construct the so-called generalized Green function. We also establish
conditions under which the main non-homogeneous problem can be
reduced to the Noetherian problem with nonzero index.
does not have eigenvalues with real part 1, we
construct the so-called generalized Green function. We also establish
conditions under which the main non-homogeneous problem can be
reduced to the Noetherian problem with nonzero index.
Submitted May 19, 2008. Published October 9, 2008.
Math Subject Classifications: 34B16, 34B05, 34B27.
Key Words: Singular boundary-value problem on the half-line;
generalized Green function; exponential dichotomy;
Noetherian operator.
Show me the
PDF file (297 KB),
TEX file, and other files for this article.
 |
Yulia Horishna
National Taras Shevchenko University of Kyiv
Faculty of Mechanics and Mathematics
Volodymyrs'ka 64, Kyiv, 01033, Ukraine
email: yuliya_g@ukr.net
|
|---|
 |
Igor Parasyuk
National Taras Shevchenko University of Kyiv
Faculty of Mechanics and Mathematics
Volodymyrs'ka 64, Kyiv, 01033, Ukraine
email: pio@mail.univ.kiev.ua
|
|---|
 |
Lyudmyla Protsak
National Pedagogical Dragomanov University
Pirogova 9, Kyiv, 01601, Ukraine
email: protsak_l_v@ukr.net
|
|---|
Return to the EJDE web page
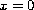 ;
these solutions should
vanish at infinity and be continuously differentiable on
;
these solutions should
vanish at infinity and be continuously differentiable on
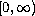 .
The resonant case where the corresponding homogeneous problem
has nontrivial solutions is of great interest to us.
Under the conditions that the homogeneous system is exponentially
dichotomic on
.
The resonant case where the corresponding homogeneous problem
has nontrivial solutions is of great interest to us.
Under the conditions that the homogeneous system is exponentially
dichotomic on
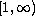 and the residue of system's
operator at
and the residue of system's
operator at
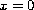 does not have eigenvalues with real part 1, we
construct the so-called generalized Green function. We also establish
conditions under which the main non-homogeneous problem can be
reduced to the Noetherian problem with nonzero index.
does not have eigenvalues with real part 1, we
construct the so-called generalized Green function. We also establish
conditions under which the main non-homogeneous problem can be
reduced to the Noetherian problem with nonzero index.


