Electron. J. Diff. Eqns., Vol. 2008(2008), No. 119, pp. 1-10.

Existence of weak solutions for a nonuniformly elliptic nonlinear system in $R^N$

Nguyen Thanh Chung

Abstract:
We study the nonuniformly elliptic, nonlinear system
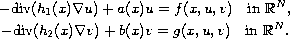
$$\displaylines{ - \hbox{div}(h_1(x)\nabla u)+ a(x)u = f(x,u,v) \quad \text{in } \mathbb{R}^N,\cr - \hbox{div}(h_2(x)\nabla v)+ b(x)v = g(x,u,v) \quad \text{in } \mathbb{R}^N. }$$
Under growth and regularity conditions on the nonlinearities f and g, we obtain weak solutions in a subspace of the Sobolev space 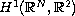$H^1(\mathbb{R}^N, \mathbb{R}^2)$ by applying a variant of the Mountain Pass Theorem.

Submitted March 27, 2008. Published August 25, 2008.
Math Subject Classifications: 35J65, 35J20.
Key Words: Nonuniformly elliptic; nonlinear systems; mountain pass theorem; weakly continuously differentiable functional.

Show me the PDF file (234 KB), TEX file, and other files for this article.

Nguyen Thanh Chung
Department of Mathematics and Informatics
Quang Binh University, 312 Ly Thuong Kiet, Dong Hoi, Vietnam
email: ntchung82@yahoo.com

Return to the EJDE web page