Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 111, pp. 1-11.
Positive solutions for an m-point boundary-value problem
Le Xuan Truong, Le Thi Phuong Ngoc, Nguyen Thanh Long
Abstract:
In this paper, we obtain sufficient conditions for the existence of
a positive solution, and infinitely many positive solutions, of the
m-point boundary-value problem
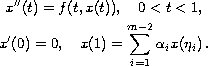
Our main tools are the Guo-Krasnoselskii's fixed point theorem
and the monotone iterative technique.
We also show that the set of positive solutions is compact.
Submitted April 22, 2008. Published August 15, 2008.
Math Subject Classifications: 34B07, 34B10, 34B18, 34B27.
Key Words: Multi-point boundary; positive solution;
Guo-Krasnoselskii fixed point theorem.
Show me the
PDF file (240 KB),
TEX file, and other files for this article.
 |
Le Xuan Truong
University of Technical Education in HoChiMinh City
01 Vo Van Ngan Str., Thu Duc Dist.,
HoChiMinh City, Vietnam
email: lxuantruong@gmail.com |
|---|
 |
Le Thi Phuong Ngoc
Nhatrang Educational College, 01 Nguyen Chanh Str.
Nhatrang City, Vietnam
email: ngoc1966@gmail.com
|
|---|
 |
Nguyen Thanh Long
Department of Mathematics and Computer Science
University of Natural Science, Vietnam National University HoChiMinh City
227 Nguyen Van Cu Str., Dist. 5, HoChiMinh City, Vietnam
email: longnt@hcmc.netnam.vn, longnt2@gmail.com
|
|---|
Return to the EJDE web page