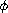 -Laplacian
type with weakly nonlinear dissipation
-Laplacian
type with weakly nonlinear dissipation
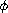 -Laplacian
type with weakly nonlinear dissipation
-Laplacian
type with weakly nonlinear dissipation
Abbes Benaissa, Aissa Guesmia
Abstract:
In this paper, first we prove the existence of global
solutions in Sobolev spaces for the initial boundary value problem
of the wave equation of
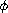 -Laplacian
with a general
dissipation of the form
-Laplacian
with a general
dissipation of the form
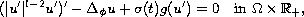
where
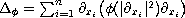 . Then we prove general
stability estimates using multiplier method and general weighted
integral inequalities proved by the second author in
[18]. Without imposing any growth condition at the
origin on
. Then we prove general
stability estimates using multiplier method and general weighted
integral inequalities proved by the second author in
[18]. Without imposing any growth condition at the
origin on
 and
and
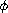 ,
we show that the energy of the system is
bounded above by a quantity, depending on
,
we show that the energy of the system is
bounded above by a quantity, depending on
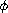 ,
,
 and
and
 ,
which tends to zero (as time approaches infinity). These
estimates allows us to consider large class of functions
,
which tends to zero (as time approaches infinity). These
estimates allows us to consider large class of functions
 and
and
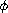 with general growth at the origin. We give some
examples to illustrate how to derive from our general estimates
the polynomial, exponential or logarithmic decay. The results of
this paper improve and generalize many existing results in the
literature, and generate some interesting open problems.
with general growth at the origin. We give some
examples to illustrate how to derive from our general estimates
the polynomial, exponential or logarithmic decay. The results of
this paper improve and generalize many existing results in the
literature, and generate some interesting open problems.
Submitted September 19, 2007. Published August 11, 2008.
Math Subject Classifications: 35B40, 35L70.
Key Words: Wave equation; global existence; general dissipative term;
rate of decay; multiplier method; integral inequalities.
Show me the PDF file (332 KB), TEX file, and other files for this article.
 |
Abbes Benaissa Department of Mathematics, Djillali Liabes University P. O. Box 89, Sidi Bel Abbes 22000, Algeria email: benaissa_abbes@yahoo.com |
|---|---|
 |
Aissa Guesmia LMAM, ISGMP, Bat. A, UFR MIM, Université Paul Verlaine - Metz Ile du Saulcy, 57045 Metz Cedex 01, France email: guesmia@univ-metz.fr |
Return to the EJDE web page