Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 10, pp. 1-18.
Blowup and life span bounds for a reaction-diffusion
equation with a time-dependent generator
Ekaterina T. Kolkovska, Jose Alfredo Lopez-Mimbela, Aroldo Perez
Abstract:
We consider the nonlinear equation
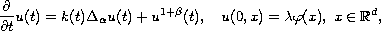
where
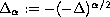 denotes the fractional power of the Laplacian;
denotes the fractional power of the Laplacian;
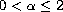 ,
,
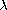 ,
,
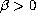 are
constants;
are
constants;
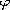 is bounded, continuous, nonnegative function
that does not vanish identically; and
is bounded, continuous, nonnegative function
that does not vanish identically; and
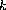 is a locally integrable function.
We prove that any combination of positive parameters
is a locally integrable function.
We prove that any combination of positive parameters
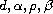 , obeying
, obeying
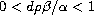 , yields
finite time blow up of any nontrivial positive solution.
Also we obtain upper and lower bounds for the life span
of the solution, and show that the life span satisfies
, yields
finite time blow up of any nontrivial positive solution.
Also we obtain upper and lower bounds for the life span
of the solution, and show that the life span satisfies
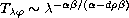 near
near
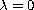 .
.
Submitted August 24, 2007. Published January 21, 2008.
Math Subject Classifications: 60H30, 35K55, 35K57, 35B35.
Key Words: Semilinear evolution equations; Feynman-Kac representation;
critical exponent; finite time blowup; nonglobal solution; life span.
Show me the
PDF file (305 KB),
TEX file, and other files for this article.
 |
Ekaterina T. Kolkovska
Centro de Investigación en Matemáticas
Apartado Postal 402, 36000 Guanajuato, Mexico
email: todorova@cimat.mx
|
|---|
 |
José Alfredo López-Mimbela
Centro de Investigación en Matemáticas
Apartado Postal 402, 36000 Guanajuato, Mexico
email: jalfredo@cimat.mx
|
|---|
 |
Aroldo Pérez Pérez
Universidad Juárez Autónoma de Tabasco
División Académica de Ciencias Básicas
Km. 1 Carretera Cunduacán-Jalpa de Méndez
C.P. 86690 A.P. 24, Cunduacán, Tabasco, Mexico
email: aroldo.perez@dacb.ujat.mx
|
|---|
Return to the EJDE web page
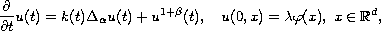
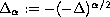 denotes the fractional power of the Laplacian;
denotes the fractional power of the Laplacian;
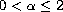 ,
,
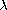 ,
,
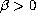 are
constants;
are
constants;
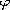 is bounded, continuous, nonnegative function
that does not vanish identically; and
is bounded, continuous, nonnegative function
that does not vanish identically; and
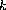 is a locally integrable function.
We prove that any combination of positive parameters
is a locally integrable function.
We prove that any combination of positive parameters
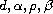 , obeying
, obeying
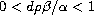 , yields
finite time blow up of any nontrivial positive solution.
Also we obtain upper and lower bounds for the life span
of the solution, and show that the life span satisfies
, yields
finite time blow up of any nontrivial positive solution.
Also we obtain upper and lower bounds for the life span
of the solution, and show that the life span satisfies
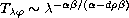 near
near
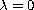 .
.


