Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 02, pp. 1-18.
Well-posedness for some perturbations of the KdV equation
with low regularity data
Xavier Carvajal, Mahendra Panthee
Abstract:
We study some well-posedness issues of the initial value problem
associated with the equation
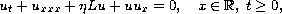
where
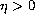 ,
,
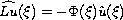 and
and
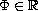 is bounded above.
Using the theory developed by Bourgain and Kenig, Ponce and Vega,
we prove that the initial value problem is locally well-posed for
given data in Sobolev spaces
is bounded above.
Using the theory developed by Bourgain and Kenig, Ponce and Vega,
we prove that the initial value problem is locally well-posed for
given data in Sobolev spaces
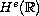 with regularity below
with regularity below
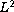 .
Examples of this model are the Ostrovsky-Stepanyams-Tsimring equation
for
.
Examples of this model are the Ostrovsky-Stepanyams-Tsimring equation
for
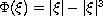 , the derivative
Korteweg-de Vries-Kuramoto-Sivashinsky equation for
, the derivative
Korteweg-de Vries-Kuramoto-Sivashinsky equation for
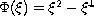 ,
and the Korteweg-de Vries-Burguers equation
for
,
and the Korteweg-de Vries-Burguers equation
for
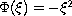 .
.
Submitted August 1, 2007. Published January 2, 2008.
Math Subject Classifications: 35A07, 35Q53.
Key Words: Bourgain spaces; KdV equation; local smoothing effect.
Show me the
PDF file (312 KB),
TEX file, and other files for this article.
 |
Xavier Carvajal
Instituto de Matemática - UFRJ
Av. Horácio Macedo, Centro de Tecnologia,
Cidade Universitária
Ilha do Fundão, Caixa Postal 68530
21941-972 Rio de Janeiro, RJ, Brasil
email: carvajal@im.ufrj.br
|
|---|
 |
Mahendra Panthee
Centro de Análise Matemática, Geometria e Sistemas
Dinâmicos
Departamento de Matemática, Instituto Superior Técnico
1049-001 Lisboa, Portugal
email: mpanthee@math.ist.utl.pt
|
|---|
Return to the EJDE web page
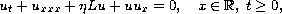
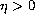 ,
,
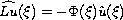 and
and
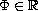 is bounded above.
Using the theory developed by Bourgain and Kenig, Ponce and Vega,
we prove that the initial value problem is locally well-posed for
given data in Sobolev spaces
is bounded above.
Using the theory developed by Bourgain and Kenig, Ponce and Vega,
we prove that the initial value problem is locally well-posed for
given data in Sobolev spaces
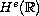 with regularity below
with regularity below
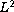 .
Examples of this model are the Ostrovsky-Stepanyams-Tsimring equation
for
.
Examples of this model are the Ostrovsky-Stepanyams-Tsimring equation
for
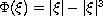 , the derivative
Korteweg-de Vries-Kuramoto-Sivashinsky equation for
, the derivative
Korteweg-de Vries-Kuramoto-Sivashinsky equation for
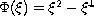 ,
and the Korteweg-de Vries-Burguers equation
for
,
and the Korteweg-de Vries-Burguers equation
for
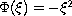 .
.

