Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 93, pp. 1-47.
Variational and topological methods for operator equations
involving duality mappings on Orlicz-Sobolev spaces
George Dinca, Pavel Matei
Abstract:
Let
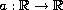 be a strictly increasing odd
continuous function with
be a strictly increasing odd
continuous function with
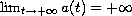 and
and
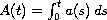 ,
,
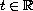 ,
the N-function
generated by a. Let
,
the N-function
generated by a. Let
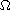 be a bounded open subset of
be a bounded open subset of
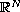 ,
,
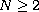 ,
,
![$T[u,u]$](gifs/ah.gif) a nonnegative quadratic form
involving the only generalized derivatives of order m of the
function
a nonnegative quadratic form
involving the only generalized derivatives of order m of the
function
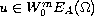 and
and
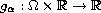 ,
,
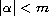 ,
be Caratheodory functions.
,
be Caratheodory functions.
We study the problem
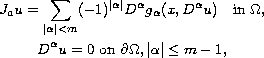
where
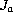 is the duality mapping on
is the duality mapping on
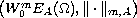 ,
subordinated
to the gauge function a (given by (1.5) and
,
subordinated
to the gauge function a (given by (1.5) and
![$$
\| u\| _{m,A}=\| \sqrt{T[u,u]}\| _{(A)},
$$](gifs/ao.gif)
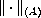 being the Luxemburg norm on
being the Luxemburg norm on
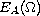 .
.
By using the Leray-Schauder topological degree and the mountain pass theorem
of Ambrosetti and Rabinowitz, the existence of nontrivial solutions is
established. The results of this paper generalize the existence results for
Dirichlet problems with p-Laplacian given in [12] and [13].
Submitted June 4, 2007. Published June 21, 2007.
Math Subject Classifications: 35B38, 35B45, 47J30, 47H11.
Key Words: A priori estimate; critical points; Orlicz-Sobolev spaces;
Leray-Schauder topological degree; Duality mapping;
Nemytskij operator; Mountain Pass Theorem.
Show me the
PDF file (559 KB),
TEX file, and other files for this article.
 |
George Dinca
Faculty of Mathematics and Computer Science,
University of Bucharest
14, Academiei Str., 010014 Bucharest, Romania
email: dinca@fmi.unibuc.ro
|
|---|
 |
Pavel Matei
Faculty of Mathematics and Computer Science,
University of Bucharest
14, Academiei Str., 010014 Bucharest, Romania
email: pavel.matei@gmail.com
|
|---|
Return to the EJDE web page
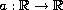 be a strictly increasing odd
continuous function with
be a strictly increasing odd
continuous function with
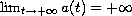 and
and
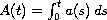 ,
,
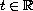 ,
the N-function
generated by a. Let
,
the N-function
generated by a. Let
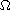 be a bounded open subset of
be a bounded open subset of
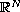 ,
,
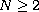 ,
,
![$T[u,u]$](gifs/ah.gif) a nonnegative quadratic form
involving the only generalized derivatives of order m of the
function
a nonnegative quadratic form
involving the only generalized derivatives of order m of the
function
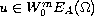 and
and
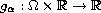 ,
,
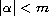 ,
be Caratheodory functions.
,
be Caratheodory functions.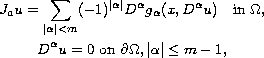
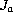 is the duality mapping on
is the duality mapping on
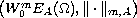 ,
subordinated
to the gauge function a (given by (1.5) and
,
subordinated
to the gauge function a (given by (1.5) and
![$$
\| u\| _{m,A}=\| \sqrt{T[u,u]}\| _{(A)},
$$](gifs/ao.gif)
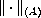 being the Luxemburg norm on
being the Luxemburg norm on
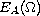 .
. 
