 -Laplacian equation
with nonlinear boundary conditions
-Laplacian equation
with nonlinear boundary conditions
 -Laplacian equation
with nonlinear boundary conditions
-Laplacian equation
with nonlinear boundary conditions
Ji-Hong Zhao, Pei-Hao Zhao
Abstract:
We study the following quasilinear problem with
nonlinear boundary conditions

where
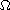 is a bounded domain in
is a bounded domain in
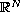 with smooth
boundary and
with smooth
boundary and
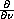 is the outer normal
derivative,
is the outer normal
derivative,
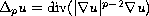 is the
p-Laplacian with 1<p<N. We consider the above problem under
several conditions on f and g, where f and g are both
Caratheodory functions. If f and g are both superlinear
and subcritical with respect to u, then we prove the existence
of infinitely many solutions of this problem by using "fountain
theorem" and "dual fountain theorem" respectively. In the case,
where g is superlinear but subcritical and f is critical with
a subcritical perturbation, namely
is the
p-Laplacian with 1<p<N. We consider the above problem under
several conditions on f and g, where f and g are both
Caratheodory functions. If f and g are both superlinear
and subcritical with respect to u, then we prove the existence
of infinitely many solutions of this problem by using "fountain
theorem" and "dual fountain theorem" respectively. In the case,
where g is superlinear but subcritical and f is critical with
a subcritical perturbation, namely
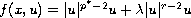 , we show that there
exists at least a nontrivial solution when
, we show that there
exists at least a nontrivial solution when
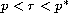 and there
exist infinitely many solutions when 1<r<p, by using
"mountain pass theorem" and "concentration-compactness principle"
respectively.
and there
exist infinitely many solutions when 1<r<p, by using
"mountain pass theorem" and "concentration-compactness principle"
respectively.
Submitted March 26, 2007. Published June 15, 2007.
Math Subject Classifications: 35J20, 35J25.
Key Words: p-Laplacian; nonlinear boundary conditions; weak solutions;
critical exponent; variational principle.
Show me the PDF file (291K), TEX file, and other files for this article.
 |
Ji-Hong Zhao Department of Mathematics Lanzhou University Lanzhou, 730000, China email: zhaojihong2007@yahoo.com.cn |
|---|---|
 |
Pei-Hao Zhao Department of Mathematics Lanzhou University Lanzhou, 730000, China email: zhaoph@lzu.edu.cn |
Return to the EJDE web page