Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 87, pp. 1-5.
A note on extremal functions for sharp Sobolev
inequalities
Ezequiel R. Barbosa, Marcos Montenegro
Abstract:
In this note we prove that any compact Riemannian manifold
of dimension
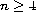 which is non-conformal to the standard
n-sphere and has positive Yamabe invariant admits infinitely
many conformal metrics with nonconstant positive scalar curvature
on which the classical sharp Sobolev inequalities admit extremal
functions. In particular we show the existence of compact Riemannian
manifolds with nonconstant positive scalar curvature for which
extremal functions exist. Our proof is simple and bases on results
of the best constants theory and Yamabe problem.
which is non-conformal to the standard
n-sphere and has positive Yamabe invariant admits infinitely
many conformal metrics with nonconstant positive scalar curvature
on which the classical sharp Sobolev inequalities admit extremal
functions. In particular we show the existence of compact Riemannian
manifolds with nonconstant positive scalar curvature for which
extremal functions exist. Our proof is simple and bases on results
of the best constants theory and Yamabe problem.
Submitted March 23, 2007. Published June 15, 2007.
Math Subject Classifications: 32Q10, 53C21.
Key Words: Extremal functions; optimal Sobolev inequalities;
conformal deformations.
Show me the
PDF file (172K),
TEX file, and other files for this article.
 |
Ezequiel R. Barbosa
Departamento de Matemática
Universidade Federal de Minas Gerais
Caixa Postal 702, 30123-970, Belo Horizonte, MG, Brazil
email: ezequiel@mat.ufmg.br
|
|---|
 |
Marcos Montenegro
Departamento de Matemática
Universidade Federal de Minas Gerais
Caixa Postal 702, 30123-970, Belo Horizonte, MG, Brazil
email: montene@mat.ufmg.br
|
|---|
Return to the EJDE web page
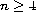 which is non-conformal to the standard
n-sphere and has positive Yamabe invariant admits infinitely
many conformal metrics with nonconstant positive scalar curvature
on which the classical sharp Sobolev inequalities admit extremal
functions. In particular we show the existence of compact Riemannian
manifolds with nonconstant positive scalar curvature for which
extremal functions exist. Our proof is simple and bases on results
of the best constants theory and Yamabe problem.
which is non-conformal to the standard
n-sphere and has positive Yamabe invariant admits infinitely
many conformal metrics with nonconstant positive scalar curvature
on which the classical sharp Sobolev inequalities admit extremal
functions. In particular we show the existence of compact Riemannian
manifolds with nonconstant positive scalar curvature for which
extremal functions exist. Our proof is simple and bases on results
of the best constants theory and Yamabe problem.

