Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 76, pp. 1-10.
Blowup and asymptotic stability of weak solutions to wave
equations with nonlinear degenerate damping and source terms
Qingying Hu, Hongwei Zhang
Abstract:
This article concerns the blow-up and asymptotic
stability of weak solutions to the wave equation
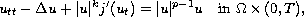
where p›1 and j' denotes the derivative of a
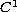 convex
and real value function j.
We prove that every weak solution is asymptotically stability,
for every m such that 0‹m‹1, p‹k+m and the the initial energy is
small; the solutions blows up in finite time, whenever p›k+m and
the initial data is positive, but appropriately bounded.
convex
and real value function j.
We prove that every weak solution is asymptotically stability,
for every m such that 0‹m‹1, p‹k+m and the the initial energy is
small; the solutions blows up in finite time, whenever p›k+m and
the initial data is positive, but appropriately bounded.
Editors note:
A reader informed us that that parts of the introduction were
copied from reference [2], without giving the proper credit.
Also that the first statement in Lemma 4.3 maybe false;
so that theorem 4.5 has not been proved.
The authors agreed to post a new proof, if they succeed in proving
the lemma.
Submitted February 27, 2007. Published May 22, 2007.
Math Subject Classifications: 35B40.
Key Words: Wave equation; degenerate damping and source terms;
asymptotic stability; blow up of solutions.
Show me the
PDF file (240K),
TEX file, and other files for this article.
 |
Qingying Hu
Department of Mathematics
Henan University of Technology
Zhengzhou 450052, China
email: slxhqy@yahoo.com.cn |
|---|
 |
Hongwei Zhang
Department of Mathematics
Henan University of Technology
Zhengzhou 450052, China
email: wei661@yahoo.com.cn |
|---|
Return to the EJDE web page
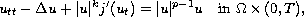
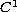 convex
and real value function j.
We prove that every weak solution is asymptotically stability,
for every m such that 0‹m‹1, p‹k+m and the the initial energy is
small; the solutions blows up in finite time, whenever p›k+m and
the initial data is positive, but appropriately bounded.
convex
and real value function j.
We prove that every weak solution is asymptotically stability,
for every m such that 0‹m‹1, p‹k+m and the the initial energy is
small; the solutions blows up in finite time, whenever p›k+m and
the initial data is positive, but appropriately bounded.

