This paper concerns the nonlinear Sturm-Liouville problem
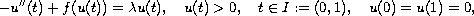
where
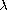 is a positive parameter. We try to determine the
nonlinear term
is a positive parameter. We try to determine the
nonlinear term
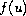 by means of the global behavior of the
bifurcation branch of the positive solutions in
by means of the global behavior of the
bifurcation branch of the positive solutions in
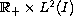 .
.
Tetsutaro Shibata
Abstract:
This paper concerns the nonlinear Sturm-Liouville problem
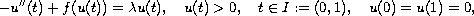
where
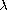 is a positive parameter. We try to determine the
nonlinear term
is a positive parameter. We try to determine the
nonlinear term
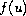 by means of the global behavior of the
bifurcation branch of the positive solutions in
by means of the global behavior of the
bifurcation branch of the positive solutions in
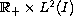 .
.
Submitted August 1, 2006. Published May 15, 2007.
Math Subject Classifications: 34B15.
Key Words: Inverse spectral problem;
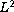 -bifurcation diagram;
logistic equations.
-bifurcation diagram;
logistic equations.
Show me the PDF file (224K), TEX file, and other files for this article.
 |
Tetsutaro Shibata Department of Applied Mathematics Graduate School of Engineering Hiroshima University Higashi-Hiroshima, 739-8527, Japan email: shibata@amath.hiroshima-u.ac.jp |
|---|
Return to the EJDE web page