Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 67, pp. 1-21.
Radial selfsimilar solutions of a nonlinear
Ornstein-Uhlenbeck equation
Arij Bouzelmate, Abdelilah Gmira, Guillermo Reyes
Abstract:
This paper concerns the existence, uniqueness and
asymptotic properties (as
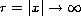 ) of radial self-similar
solutions to the nonlinear Ornstein-Uhlenbeck equation
) of radial self-similar
solutions to the nonlinear Ornstein-Uhlenbeck equation
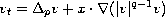
in
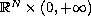 . Here
. Here
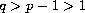 ,
,
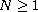 ,
and
,
and
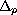 denotes the
denotes the
 -Laplacian operator.
These solutions are of the form
-Laplacian operator.
These solutions are of the form
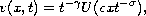
where
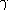 and
and
 are fixed powers given by the
invariance properties of differential equation, while
are fixed powers given by the
invariance properties of differential equation, while
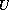 is a radial
function,
is a radial
function,
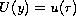 ,
,
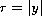 .
With the choice
.
With the choice
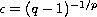 ,
the radial profile
,
the radial profile
 satisfies the nonlinear ordinary differential
equation
satisfies the nonlinear ordinary differential
equation
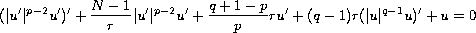
in
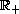 .
We carry out a careful analysis of this equation and
deduce the corresponding consequences for the Ornstein-Uhlenbeck equation.
.
We carry out a careful analysis of this equation and
deduce the corresponding consequences for the Ornstein-Uhlenbeck equation.
Submitted January 11, 2007. Published May 9, 2007.
Math Subject Classifications: 34L30, 35K55, 35K65.
Key Words: p-laplacian; Ornstein-Uhlenbeck diffusion equations;
self-similar solutions; shooting technique.
Show me the
PDF file (337K),
TEX file, and other files for this article.
 |
Arij Bouzelmate
Département de Mathématiques et Informatique
Faculté des Sciences, BP 2121, Tétouan, Maroc
email: bouzelmatearij@yahoo.fr |
|---|
 |
Abdelilah Gmira
Département de Mathématiques et Informatique
Faculté des Sciences, BP 2121, Tétouan, Maroc
email: gmira@fst.ac.ma or gmira.i@menara.ma |
|---|
| |
Guillermo Reyes
Departamento de Matemáticas
Universidad Carlos III de Madrid, Leganés, Madrid 28911, Spain
email: greyes@math.uc3m.es |
|---|
Return to the EJDE web page
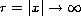 ) of radial self-similar
solutions to the nonlinear Ornstein-Uhlenbeck equation
) of radial self-similar
solutions to the nonlinear Ornstein-Uhlenbeck equation
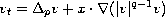
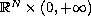 . Here
. Here
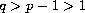 ,
,
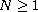 ,
and
,
and
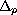 denotes the
denotes the
 -Laplacian operator.
These solutions are of the form
-Laplacian operator.
These solutions are of the form
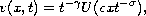
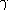 and
and
 are fixed powers given by the
invariance properties of differential equation, while
are fixed powers given by the
invariance properties of differential equation, while
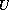 is a radial
function,
is a radial
function,
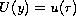 ,
,
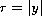 .
With the choice
.
With the choice
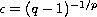 ,
the radial profile
,
the radial profile
 satisfies the nonlinear ordinary differential
equation
satisfies the nonlinear ordinary differential
equation
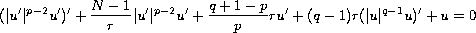
 .
We carry out a careful analysis of this equation and
deduce the corresponding consequences for the Ornstein-Uhlenbeck equation.
.
We carry out a careful analysis of this equation and
deduce the corresponding consequences for the Ornstein-Uhlenbeck equation.

