Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 64, pp. 1-11.
Asymptotic shape of solutions to
the perturbed simple pendulum problems
Tetsutaro Shibata
Abstract:
We consider the positive solution of
the perturbed simple pendulum problem
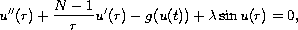
with
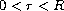 ,
,
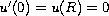 .
To understand well
the shape of the solution
.
To understand well
the shape of the solution
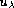 when
when
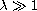 ,
we establish the leading and second terms of
,
we establish the leading and second terms of
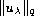 (
(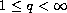 ) with the estimate of third term as
) with the estimate of third term as
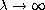 .
We also obtain the asymptotic formula for
.
We also obtain the asymptotic formula for
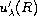 as
as
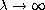 .
.
Submitted May 12, 2006. Published May 9, 2007.
Math Subject Classifications: 35J60.
Key Words: Asymptotic formulas; Lq-norm; simple pendulum.
Show me the
PDF file (232K),
TEX file, and other files for this article.
 |
Tetsutaro Shibata
Department of Applied Mathematics
Graduate School of Engineering
Hiroshima University
Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
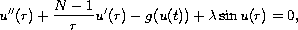
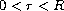 ,
,
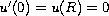 .
To understand well
the shape of the solution
.
To understand well
the shape of the solution
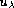 when
when
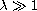 ,
we establish the leading and second terms of
,
we establish the leading and second terms of
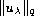 (
(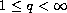 ) with the estimate of third term as
) with the estimate of third term as
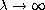 .
We also obtain the asymptotic formula for
.
We also obtain the asymptotic formula for
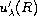 as
as
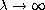 .
.
