Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 62, pp. 1-5.
Forced oscillations for delay motion equations on manifolds
Pierluigi Benevieri, Alessandro Calamai,
Massimo Furi, Maria Patrizia Pera
Abstract:
We prove an existence result for
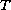 -periodic solutions of a
-periodic solutions of a
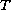 -periodic second order delay differential equation on a
boundaryless compact manifold with nonzero Euler-Poincare
characteristic. The approach is based on an existence result
recently obtained by the authors for first order delay differential
equations on compact manifolds with boundary.
-periodic second order delay differential equation on a
boundaryless compact manifold with nonzero Euler-Poincare
characteristic. The approach is based on an existence result
recently obtained by the authors for first order delay differential
equations on compact manifolds with boundary.
Submitted July 29, 2006. Published April 26, 2007.
Math Subject Classifications: 34K13, 37C25.
Key Words: Delay differential equations; Forced oscillations;
periodic solutions; compact manifolds;
Euler-Poincare characteristic; fixed point index.
Show me the
PDF file (173K),
TEX file, and other files for this article.
 |
Pierluigi Benevieri
Dipartimento di Matematica Applicata "Giovanni Sansone"
Università degli Studi di Firenze
Via S. Marta 3,
I-50139 Firenze, Italy
email: pierluigi.benevieri@unifi.it |
|---|
 |
Alessandro Calamai
Dipartimento di Scienze Matematiche
Università Politecnica delle Marche
Via Brecce Bianche,
I-60131 Ancona, Italy
email: calamai@math.unifi.it, calamai@dipmat.univpm.it |
|---|
 |
Massimo Furi
Dipartimento di Matematica Applicata "Giovanni Sansone"
Università degli Studi di Firenze
Via S. Marta 3,
I-50139 Firenze, Italy
email: massimo.furi@unifi.it
|
|---|
 |
Maria Patrizia Pera
Dipartimento di Matematica Applicata "Giovanni Sansone"
Università degli Studi di Firenze
Via S. Marta 3,
I-50139 Firenze, Italy
email: mpatrizia.pera@unifi.it
|
|---|
Return to the EJDE web page
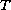 -periodic solutions of a
-periodic solutions of a
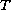 -periodic second order delay differential equation on a
boundaryless compact manifold with nonzero Euler-Poincare
characteristic. The approach is based on an existence result
recently obtained by the authors for first order delay differential
equations on compact manifolds with boundary.
-periodic second order delay differential equation on a
boundaryless compact manifold with nonzero Euler-Poincare
characteristic. The approach is based on an existence result
recently obtained by the authors for first order delay differential
equations on compact manifolds with boundary.



