Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 49, pp. 1-13.
Positive periodic solutions for the Korteweg-de Vries equation
Svetlin Georgiev Georgiev
Abstract:
In this paper we prove that the Korteweg-de Vries equation
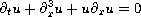
has unique positive solution
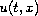 which is
which is
 -periodic
with respect to the time variable
-periodic
with respect to the time variable
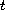 and
and
![$u(0, x)\in {\dot B}^{\gamma}_{p, q}([a, b])$](gifs/ae.gif) ,
,
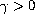 ,
,
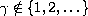 ,
,
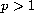 ,
,
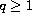 ,
,
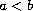 are fixed constants,
are fixed constants,
![$x\in [a, b]$](gifs/ak.gif) .
The period
.
The period
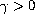 is arbitrary chosen and fixed.
is arbitrary chosen and fixed.
Submitted January 18, 2006. Published April 4, 2007.
Math Subject Classifications: 35Q53, 35Q35, 35G25
Key Words: Nonlinear evolution equation; Kortewg de Vries equation;
periodic solutions.
Show me the
PDF file (234K),
TEX file, and other files for this article.
 |
Svetlin Georgiev Georgiev
Department of Differential Equations
University of Sofia, Sofia, Bulgaria
email: sgg2000bg@yahoo.com |
|---|
Return to the EJDE web page
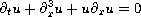
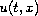 which is
which is
 -periodic
with respect to the time variable
-periodic
with respect to the time variable
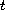 and
and
![$u(0, x)\in {\dot B}^{\gamma}_{p, q}([a, b])$](gifs/ae.gif) ,
,
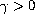 ,
,
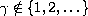 ,
,
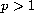 ,
,
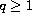 ,
,
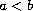 are fixed constants,
are fixed constants,
![$x\in [a, b]$](gifs/ak.gif) .
The period
.
The period
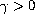 is arbitrary chosen and fixed.
is arbitrary chosen and fixed.
