Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 48, pp. 1-19.
Existence and asymptotic expansion of solutions
to a nonlinear wave equation with a memory condition
at the boundary
Nguyen Thanh Long, Le Xuan Truong
Abstract:
We study the initial-boundary value problem for the nonlinear
wave equation
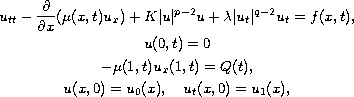
where
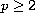 ,
,
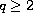 ,
,
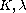 are given constants and
are given constants and
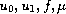 are given functions. The unknown function
are given functions. The unknown function
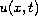 and the unknown boundary value
and the unknown boundary value
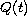 satisfy the
linear integral equation
satisfy the
linear integral equation
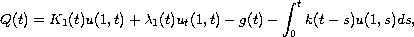
where
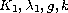 are given functions satisfying some
properties stated in the next section. This paper consists of two
main sections. First, we prove the existence and uniqueness for
the solutions in a suitable function space. Then, for the case
are given functions satisfying some
properties stated in the next section. This paper consists of two
main sections. First, we prove the existence and uniqueness for
the solutions in a suitable function space. Then, for the case
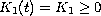 ,
we find the asymptotic expansion in
,
we find the asymptotic expansion in
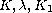 of the solutions, up to order
of the solutions, up to order
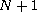 .
.
Submitted October 27, 2006. Published March 20, 2007.
Math Subject Classifications: 35L20, 35L70.
Key Words: Nonlinear wave equation; linear integral equation;
existence and uniqueness; asymptotic expansion.
Show me the
PDF file (308K),
TEX file, and other files for this article.
 |
Nguyen Thanh Long
Department of Mathematics
Hochiminh City National University
227 Nguyen Van Cu, Q5, HoChiMinh City, Vietnam
email: longnt@hcmc.netnam.vn, longnt2@gmail.com
|
|---|
 |
Le Xuan Truong
Department of Mathematics, Faculty of General Science
University of Technical Education in HoChiMinh City
01 Vo Van Ngan Str., Thu Duc Dist., HoChiMinh City, Vietnam
email: lxuantruong@gmail.com
|
|---|
Return to the EJDE web page
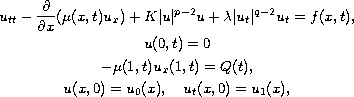
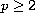 ,
,
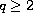 ,
,
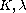 are given constants and
are given constants and
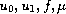 are given functions. The unknown function
are given functions. The unknown function
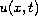 and the unknown boundary value
and the unknown boundary value
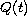 satisfy the
linear integral equation
satisfy the
linear integral equation
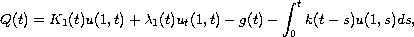
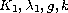 are given functions satisfying some
properties stated in the next section. This paper consists of two
main sections. First, we prove the existence and uniqueness for
the solutions in a suitable function space. Then, for the case
are given functions satisfying some
properties stated in the next section. This paper consists of two
main sections. First, we prove the existence and uniqueness for
the solutions in a suitable function space. Then, for the case
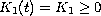 ,
we find the asymptotic expansion in
,
we find the asymptotic expansion in
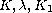 of the solutions, up to order
of the solutions, up to order
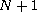 .
.

