Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 27, pp. 1-12.
Periodicity and stability in neutral nonlinear dynamic equations
with functional delay on a time scale
Eric R. Kaufmann, Youssef N. Raffoul
Abstract:
Let
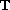 be a periodic time scale. We use a
fixed point theorem due to Krasnosel'skii to show that the
nonlinear neutral dynamic equation with delay
be a periodic time scale. We use a
fixed point theorem due to Krasnosel'skii to show that the
nonlinear neutral dynamic equation with delay

has a periodic solution. Under a slightly
more stringent inequality we show that the periodic solution is
unique using the contraction mapping principle. Also, by the aid
of the contraction mapping principle we study the asymptotic stability of
the zero solution provided that
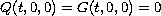 .
.
Submitted July 11, 2006. Published February 12, 2007.
Math Subject Classifications: 34K13, 34C25, 34G20.
Key Words: Krasnosel'skii; contraction mapping; neutral;
nonlinear; Delay; time scales; periodic solution;
unique solution; stability.
Show me the
PDF file (256K),
TEX file, and other files for this article.
 |
Eric R. Kaufmann
Department of Mathematics and Statistics
University of Arkansas at Little Rock
Little Rock, Arkansas 72204-1099, USA
email: erkaufmann@ualr.edu
|
|---|
 |
Youssef N. Raffoul
Department of Mathematics,
University of Dayton
Dayton, OH 45469-2316, USA
e-mail: youssef.raffoul@notes.udayton.edu |
|---|
Return to the EJDE web page
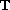 be a periodic time scale. We use a
fixed point theorem due to Krasnosel'skii to show that the
nonlinear neutral dynamic equation with delay
be a periodic time scale. We use a
fixed point theorem due to Krasnosel'skii to show that the
nonlinear neutral dynamic equation with delay

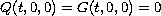 .
.

