Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 22, pp. 1-5.
On asymptotic behaviour of oscillatory solutions for
fourth order differential equations
Seshadev Padhi, Chuanxi Qian
Abstract:
We establish sufficient conditions for the linear differential
equations of fourth order

so that all oscillatory solutions of the equation satisfy
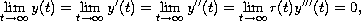
where
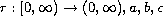 and
and
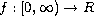 are continuous functions. A suitable Green's function and its
estimates are used in this paper.
are continuous functions. A suitable Green's function and its
estimates are used in this paper.
Submitted December 2, 2006. Published February 4, 2007.
Math Subject Classifications: 34C10.
Key Words: Oscillatory solution; asymptotic behaviour.
Show me the
PDF file (179K),
TEX file, and other files for this article.
 |
Seshadev Padhi
Department of Applied Mathematics
Birla Institute of Technology,
Mesra, Ranchi -835 215, India
email: ses_2312@yahoo.co.in |
|---|
 |
Chuanxi Qian
Department of Mathematics and Statistics
Mississippi State University
Mississippi state, MS 39762, USA
email: qian@math.msstate.edu |
|---|
Return to the EJDE web page

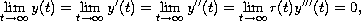
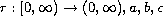 and
and
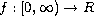 are continuous functions. A suitable Green's function and its
estimates are used in this paper.
are continuous functions. A suitable Green's function and its
estimates are used in this paper.

