We prove global well-posedness for the radial defocusing cubic wave equation
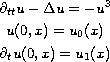
with data
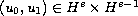 ,
,
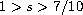 .
The proof relies upon a Morawetz-Strauss-type
inequality that allows us to control the growth of an almost
conserved quantity.
.
The proof relies upon a Morawetz-Strauss-type
inequality that allows us to control the growth of an almost
conserved quantity.
Tristan Roy
Abstract:
We prove global well-posedness for the radial defocusing cubic
wave equation
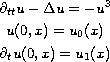
with data
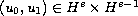 ,
,
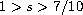 .
The proof relies upon a Morawetz-Strauss-type
inequality that allows us to control the growth of an almost
conserved quantity.
.
The proof relies upon a Morawetz-Strauss-type
inequality that allows us to control the growth of an almost
conserved quantity.
Submitted August 17, 2007. Published November 30, 2007.
Math Subject Classifications: 35Q55
Key Words: Nonlinear Schrodinger equation; well-posedness
Show me the PDF file (355 KB), TEX file, and other files for this article.
 |
Tristan Roy UCLA Mathematics Department, Box 951555 Los Angeles, CA 90095-1555, USA email: triroy@math.ucla.edu |
|---|
Return to the EJDE web page