Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 164, pp. 1-18.
A Neumann problem with the q-Laplacian on a solid torus
in the critical of supercritical case
Athanase Cotsiolis, Nikos Labropoulos
Abstract:
Following the work of Ding [21] we study the existence of
a nontrivial positive solution to the nonlinear Neumann problem
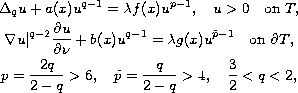
on a solid torus of R3. When data are invariant under
the group
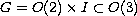 , we find solutions
that exhibit no radial symmetries.
First we find the best constants in the Sobolev inequalities for
the supercritical case (the critical of supercritical).
, we find solutions
that exhibit no radial symmetries.
First we find the best constants in the Sobolev inequalities for
the supercritical case (the critical of supercritical).
Submitted May 18, 2006. Published November 30, 2007.
Math Subject Classifications: 35J65, 46E35, 58D19.
Key Words: Neumann problem; q-Laplacian; solid torus; no radial symmetry;
critical of supercritical exponent.
Show me the
PDF file (310 KB),
TEX file, and other files for this article.
 |
Athanase Cotsiolis
Department of Mathematics, University of Patras
Patras 26110, Greece
email: cotsioli@math.upatras.gr |
|---|
 |
Nikos Labropoulos
Department of Mathematics, University of Patras
Patras 26110, Greece
email: nal@upatras.gr |
|---|
Return to the EJDE web page
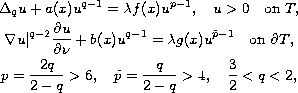
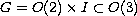 , we find solutions
that exhibit no radial symmetries.
First we find the best constants in the Sobolev inequalities for
the supercritical case (the critical of supercritical).
, we find solutions
that exhibit no radial symmetries.
First we find the best constants in the Sobolev inequalities for
the supercritical case (the critical of supercritical).

