Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 163, pp. 1-14.
Non-oscillatory behaviour of higher order functional
differential equations of neutral type
Radhanath Rath, Niyati Misra,
Prayag Prasad Mishra, Laxmi Narayan Padhy
Abstract:
In this paper, we obtain sufficient conditions so that the
neutral functional differential equation
![$$\displaylines{
\big[r(t) [y(t)-p(t)y(\tau (t))]'\big]^{(n-1)} +
q(t) G(y(h(t))) = f(t)
}$$](gifs/aa.gif)
has a bounded and positive solution.
Here
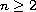 ;
;
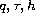 are continuous functions
with
are continuous functions
with
 ;
;
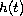 and
and
 are increasing functions which are less than
are increasing functions which are less than
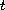 ,
and approach infinity as
,
and approach infinity as
 .
In our work,
.
In our work,
 is admissible, and neither we assume
that
is admissible, and neither we assume
that
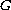 is non-decreasing, that
is non-decreasing, that
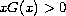 for
for
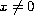 ,
nor that
,
nor that
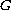 is Lipschitzian. Hence the results of this paper generalize
many results in [1] and [4]-[8].
is Lipschitzian. Hence the results of this paper generalize
many results in [1] and [4]-[8].
Submitted September 24, 2007. Published November 30, 2007.
Math Subject Classifications: 34C10, 34C15, 34K40.
Key Words: Oscillatory solution; nonoscillatory solution;
asymptotic behaviour.
Show me the
PDF file (262 KB),
TEX file, and other files for this article.
 |
Radhanath Rath
Department of Mathematics
Khallikote Autonomous College
Berhampur, 760001 Orissa, India
email: radhanathmath@yahoo.co.in |
|---|
 |
Niyati Misra
Department of Mathematics
Berhampur University
Berhampur, 760007 Orissa, India
email: niyatimath@yahoo.co.in |
|---|
 |
Prayag Prasad Mishra
Department of Mathematics
Silicin Institute of Technology
Bhubaneswar, Orissa, India
email: prayag@silicon.ac.in |
|---|
 |
Laxmi Narayan Padhy
Department of Computer Science and Engineering, K.I.S.T,
Bhubaneswar Orissa, India
email: ln_padhy_2006@yahoo.co.in |
|---|
Return to the EJDE web page
![$$\displaylines{
\big[r(t) [y(t)-p(t)y(\tau (t))]'\big]^{(n-1)} +
q(t) G(y(h(t))) = f(t)
}$$](gifs/aa.gif)
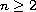 ;
;
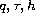 are continuous functions
with
are continuous functions
with
 ;
;
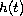 and
and
 are increasing functions which are less than
are increasing functions which are less than
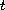 ,
and approach infinity as
,
and approach infinity as
 .
In our work,
.
In our work,
 is admissible, and neither we assume
that
is admissible, and neither we assume
that
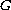 is non-decreasing, that
is non-decreasing, that
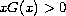 for
for
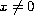 ,
nor that
,
nor that
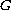 is Lipschitzian. Hence the results of this paper generalize
many results in [1] and [4]-[8].
is Lipschitzian. Hence the results of this paper generalize
many results in [1] and [4]-[8].



