Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 16, pp. 1-8.
Positive solutions for semipositone fourth-order
two-point boundary value problems
Dandan Yang, Hongbo Zhu, Chuanzhi Bai
Abstract:
In this paper we investigate the existence of positive solutions of
the following nonlinear semipositone fourth-order two-point
boundary-value problem with second derivative:

where
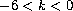 ,
,
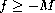 , and
, and
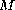 is a positive constant.
Our approach relies on the Krasnosel'skii fixed point theorem.
is a positive constant.
Our approach relies on the Krasnosel'skii fixed point theorem.
Submitted August 3, 2006. Published January 23, 2007.
Math Subject Classifications: 34B16.
Key Words: Boundary value problem; Positive solution;
semipositone; fixed point
Show me the
PDF file (185K),
TEX file, and other files for this article.
 |
Dandan Yang
Department of Mathematics, Yanbian University
Yanji, Jilin 133000, China.
Department of Mathematics, Huaiyin Teachers College
Huaian, Jiangsu 223001, China
email: yangdandan2600@sina.com
|
|---|
 |
Hongbo Zhu
Department of Mathematics, Yanbian University
Yanji, Jilin 133000, China.
Department of Mathematics, Huaiyin Teachers College
Huaian, Jiangsu 223001, China
email: zhuhongbo8151@sina.com
|
|---|
 |
Chuanzhi Bai
Department of Mathematics
Huaiyin Teachers College
Huaian, Jiangsu 223001, China
email: czbai8@sohu.com
|
|---|
Return to the EJDE web page

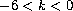 ,
,
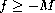 , and
, and
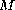 is a positive constant.
Our approach relies on the Krasnosel'skii fixed point theorem.
is a positive constant.
Our approach relies on the Krasnosel'skii fixed point theorem.


