 ,
Part 1: convex corners
,
Part 1: convex corners
 ,
Part 1: convex corners
,
Part 1: convex corners
Thalia Jeffres, Kirk Lancaster
Abstract:
One technique which is useful in the calculus of
variations is that of "blowing up". This technique can
contribute to the understanding of the boundary behavior of
solutions of boundary value problems, especially when they involve
mean curvature and a contact angle boundary condition. Our goal in
this note is to investigate the structure of "blown up" sets of
the form
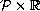 and
and
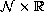 when
when
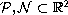 and
and
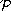 (or
(or
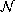 )
minimizes an appropriate functional; sets
like
)
minimizes an appropriate functional; sets
like
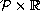 can be the limits of the blow
ups of subgraphs of solutions of mean curvature problems, for example.
In Part One, we investigate "blown up" sets when the domain has
a convex corner. As an application, we illustrate the second author's
proof of the Concus-Finn Conjecture by providing a simplified proof
when the mean curvature is zero.
can be the limits of the blow
ups of subgraphs of solutions of mean curvature problems, for example.
In Part One, we investigate "blown up" sets when the domain has
a convex corner. As an application, we illustrate the second author's
proof of the Concus-Finn Conjecture by providing a simplified proof
when the mean curvature is zero.
Submitted January 9, 2007. Published November 13, 2007.
Math Subject Classifications: 49Q20, 53A10, 76B45.
Key Words: Blow-up sets; capillary surface; Concus-Finn conjecture.
Show me the PDF file (358 KB), TEX file, and other files for this article.
 |
Thalia Jeffres Department of Mathematics and Statistics Wichita State University Wichita, Kansas, 67260-0033, USA email: jeffres@math.wichita.edu |
|---|---|
 |
Kirk Lancaster Department of Mathematics and Statistics Wichita State University Wichita, Kansas, 67260-0033, USA email: lancaster@math.wichita.edu |
Return to the EJDE web page